A point mass m starts to slide from rest from the top of a smooth solid sphere of radius r. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and sphere, does the mass fly off at a greater or lesser angle ?
The correct Answer is:48∘12' ; greater angle
Step by step video, text & image solution for A point mass m starts to slide from rest from the top of a smooth solid sphere of radius r. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and sphere, does the mass fly off at a greater or lesser angle ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRIPITAL AND CENTRIFUGAL FORCESBook:NN GHOSHChapter:CENTRIPITAL AND CENTRIFUGAL FORCESExercise:Exercises (A)
Explore 18 Videos
- CALORIMETRYBook:NN GHOSHChapter:CALORIMETRYExercise:All Questions
Explore 28 Videos
- COMPOSITION AND RESOLUTION OF VELOCITIESBook:NN GHOSHChapter:COMPOSITION AND RESOLUTION OF VELOCITIESExercise:Exercise
Explore 25 Videos
Similar Questions
A point mass m starts from rest and slides down the surface of a frictionless hemisphere of radius r as shown figure. Measure angle from the vertical and potential energy from the top. Find
a. Find the changes in potential energy of the mass with angle
b. Find the kinetic energy as a function of angle
c. Find the radial and tangential acceleration as a function of angle
d. Find the angle at which the mass files off the hemisphere
e. If there is friction between the mass and hemisphere, does the mass fly off at a greater or lesser angle than in part (d) ?
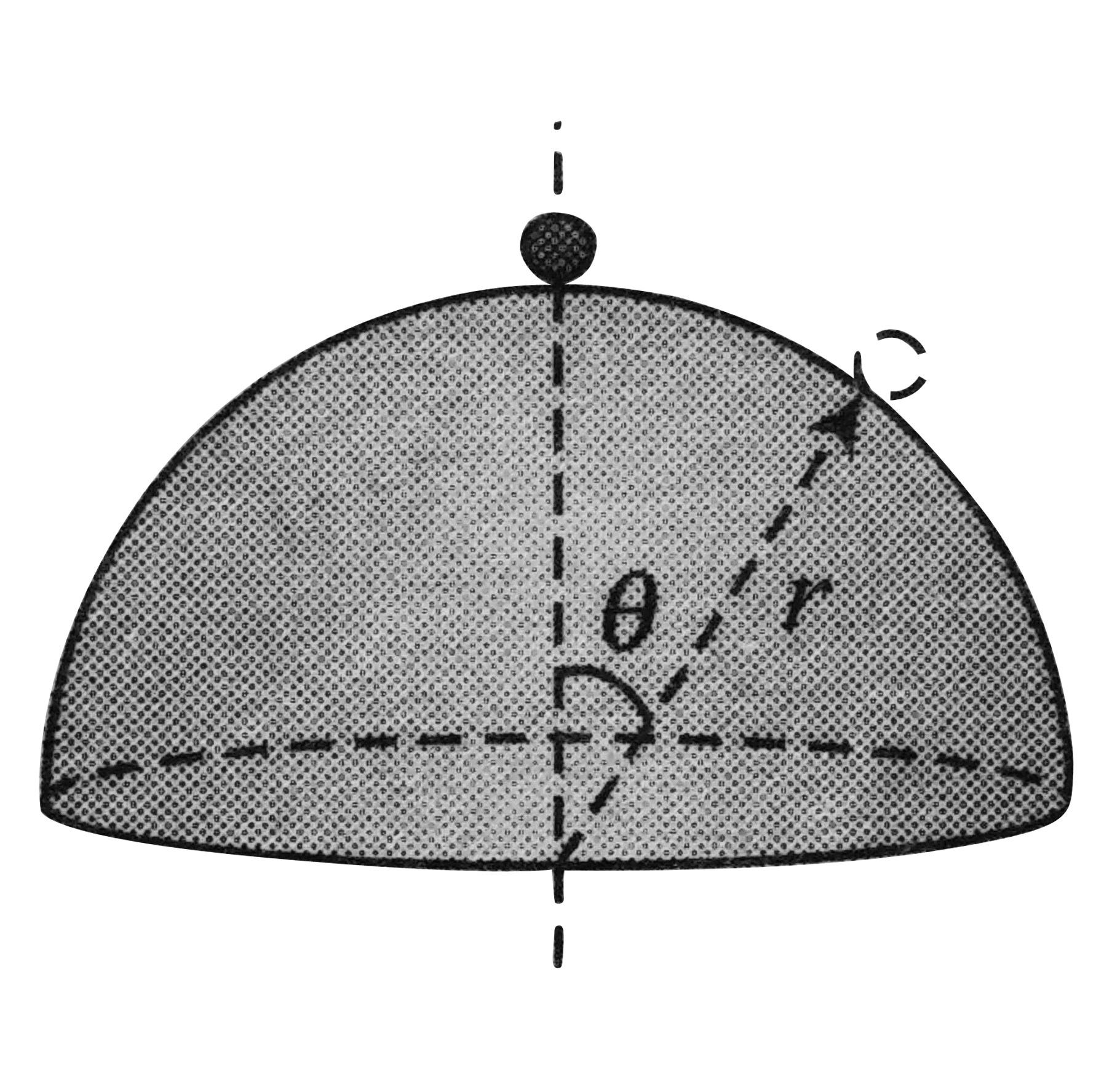
View SolutionA small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.

View Solution
Knowledge Check
A particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
A2g3B√5g3CgDg3The moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A25MR2B63MR2C45MR2D75MR2A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
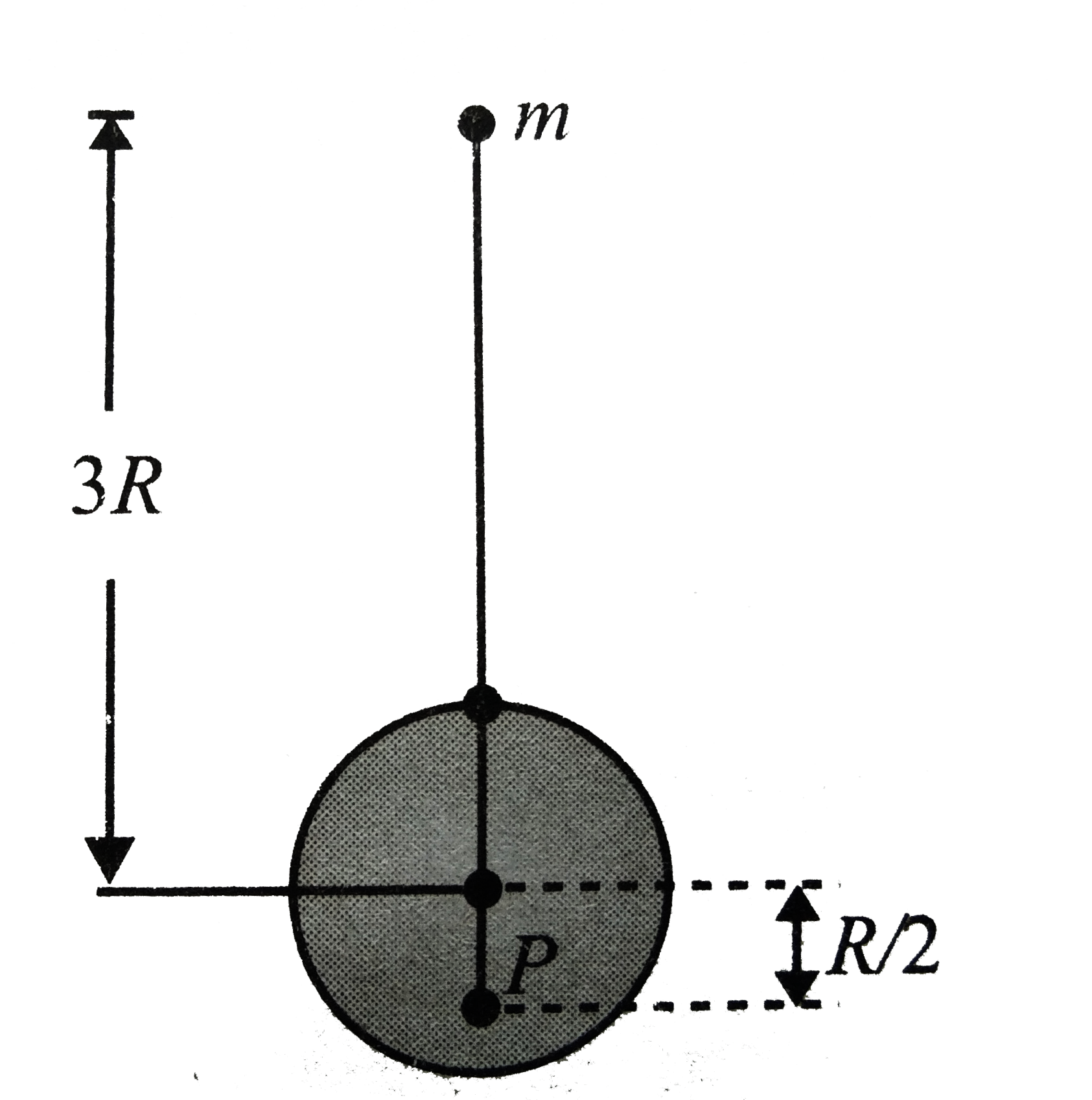 A√2GM3RB√5GM3RC√25GM24RDnone of these
A√2GM3RB√5GM3RC√25GM24RDnone of these
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA particle of mass m being to slide down a fixed smooth sphere from the top as shown. If its acceleration when it breaks off the sphere is 2a. The value of a is :
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View SolutionA solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
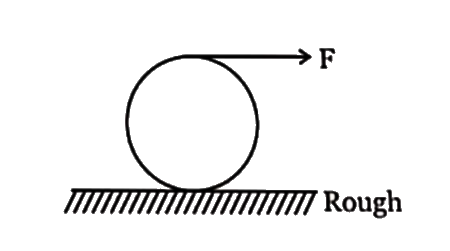
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View Solution

