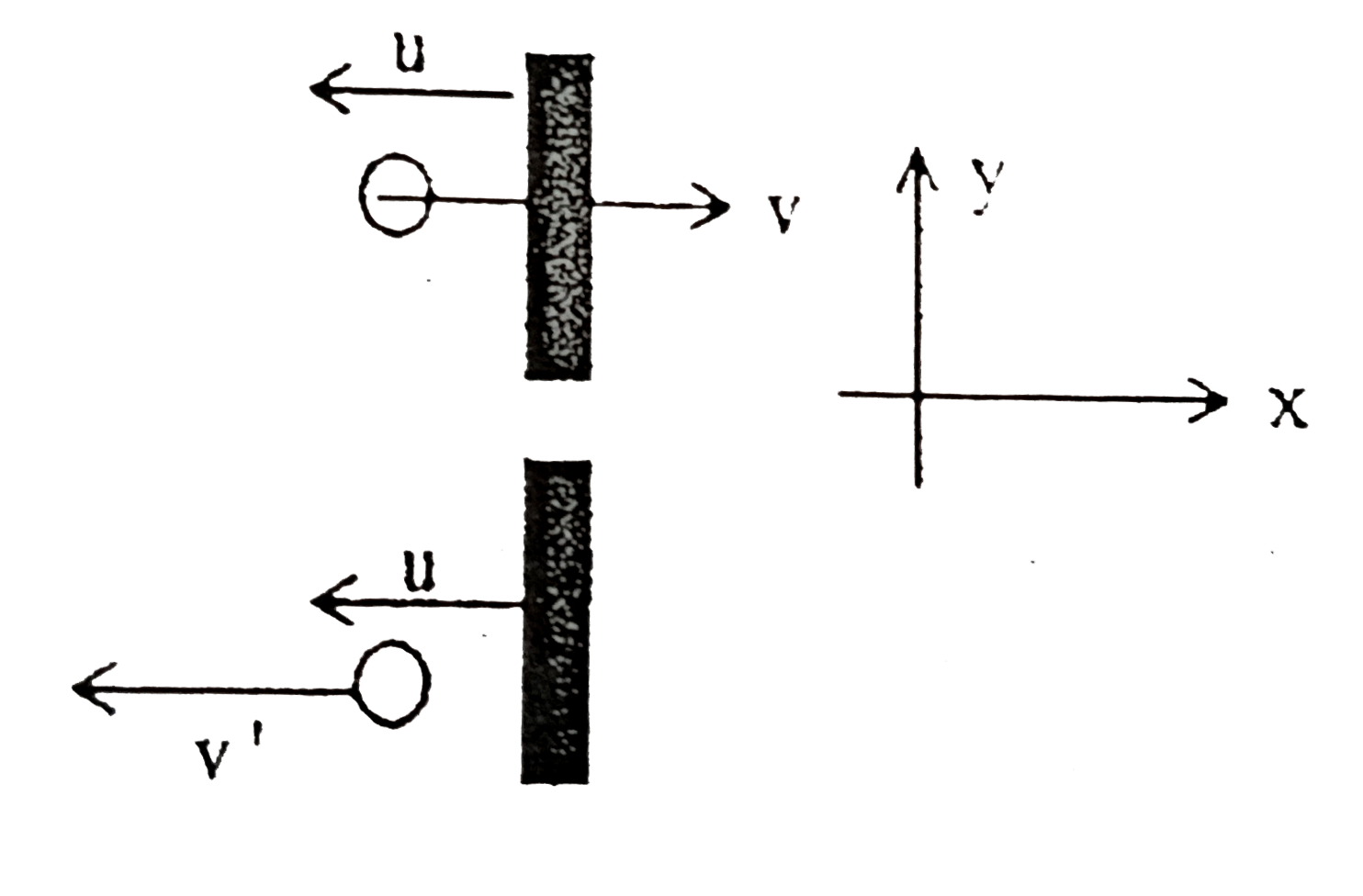
A particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
(1/2)m(u+v)2
(1/2)m(u+v)
(1/2)μv
2μ(u+v)
Velocity of separation =−e (velocity of approach)
⇒(−v'i)−(ui)=−e[(vi)−(−ui)]
⇒u−v'=−1(v+u)
⇒v'=2u+v
∴W=ΔK.E.=12mv'2−12mv2
=12m[(2u+v)2−v2]=2μ(u+v)
Topper's Solved these Questions
Similar Questions
For a particle moving in a horizontal circle with constant angular velocity:
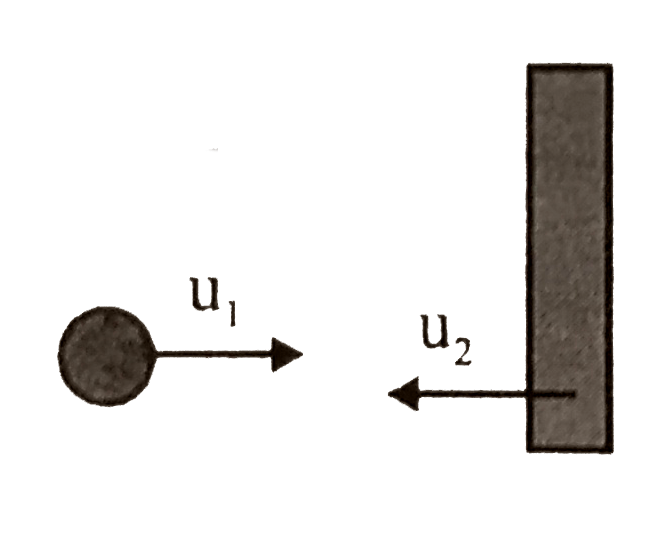
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
View Solution
Knowledge Check
A particle is moving horizontally with constant acceleration.
AThe sum of the horizontal components of the forces acting on the particle is not zero.BThe sum of the vertical component of the forces acting on the particle is not zero.CThe forces acting on the particle are not in equilibrium.DAll of the above.A particle is moving in a circle with a constant speed. Its moving is
APeriodicBOscillatoryCSimple harmonicDboth 'a' and 'b'A particle is moving in a horizontal circle with constant speed. It has constant
AVelocityBaccelerationCKinetic energyDDisplacement
A particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View SolutionA particle of mass m1 moving with velocity v in a positive direction collides elastically with a mass m2 moving in opposite direction also at velocity v. If m2>>m1, then
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
View Solution

