In the figure shown a semi-cylinder of radius, R is rigidly fixed on a horizontal table of height l0 from the ground such that there is a common edge of the table and semi-cylinder. A block of mss m is attached rigidly to a light spring of stiffnes k, whose other end is rigidly attached to the ground. The natural length of the spring is l0. A force of constant magnitude F is applied on the block to move it on the frictionless surface of the semi-cylinder in a vertical plane such that the path followed by the block is a semicircle of radius R.
The force F is always tangential to the cylinder. Find the contact force between the cylinder and the block as a function of θ, Initial speed of the block is zero and initial length of the spring is l0.0 is the angular displacement of the block w.r.t. the centre of the circular path as shown in the figure.
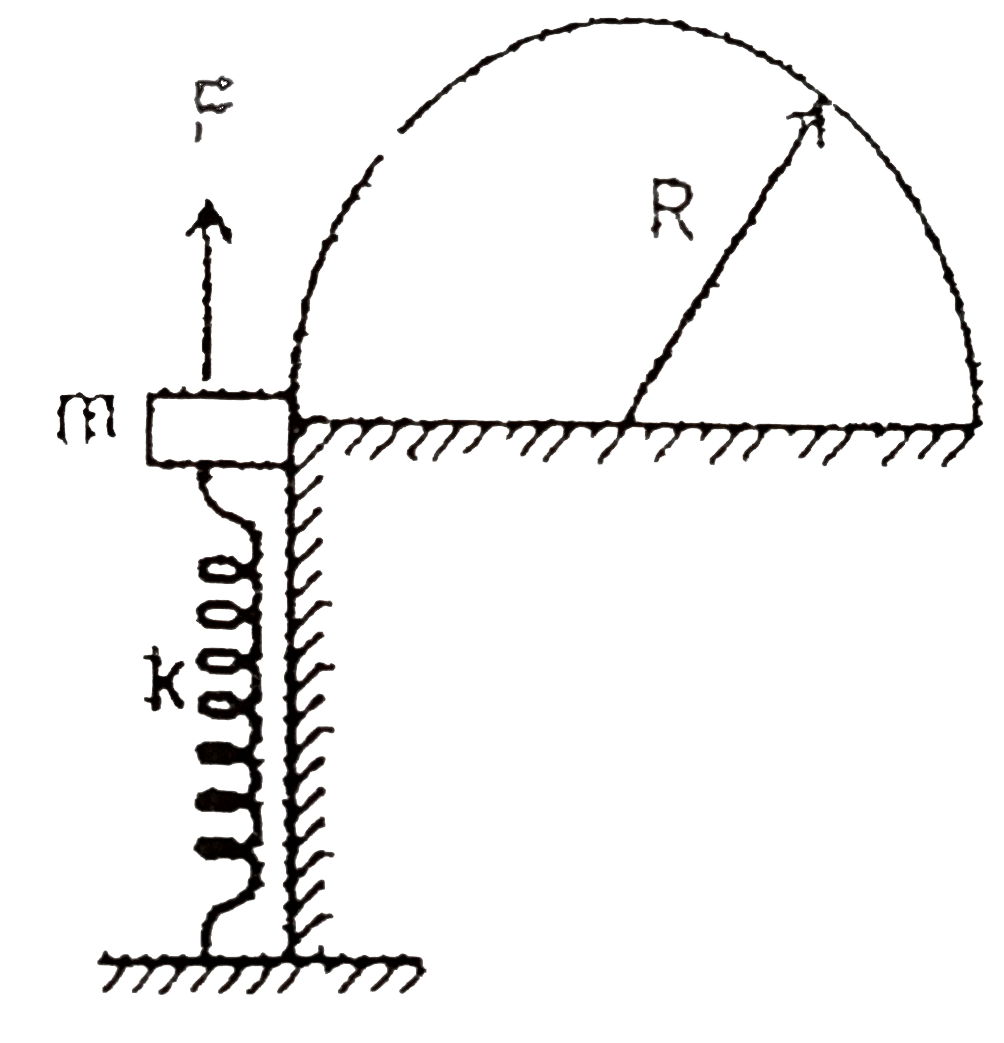
WN= work done by normal reaction =0
Wg=−mgRsinθ
Wspring=−12k(Rθ)2
WF=FRθ
ΣW=ΔKE
⇒−mgRsinθ−12kR2θ2+FRθ=12mv2
⇒mv2=−2mgRsinθ−kR2θ2+2FRθ......(i)
Also, mgsinθ−N=mv2R
⇒N=mgsinθ−mv2R
=mgsinθ+2mgsinθ+kRθ2−2Fθ using equation (i)
=3mgsinθ+kRθ2−2Fθ

Topper's Solved these Questions
Similar Questions
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View Solution
A block of mass m is pressed against a horizontal spring fixed at one end to compress the spring through (L0)/(2). The natural length of the spring is L0 and spring constant k=(mg)/(L0). When released, the block moves horizontally on smooth surface till it leaves the spring. At what horizontal distance from O it strikes the ground.
View Solution
Knowledge Check
A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπA block is attached to a spring of stiffness k. The other end of the spring is attached to a fixed wall. The entire system lie on a horizontal surface and the spring is in natural state. The natural length of the springs is l0 if the block is slowly lifted up vertically to a height 512l0 from its initial position :
AThe work done by the lifting force =kl20288+512mgl0BThe work done by the spring force =kl20288CThe work done by the gravity =512mgl0DThe work done by lifting force =−512mgl0+kl20288A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
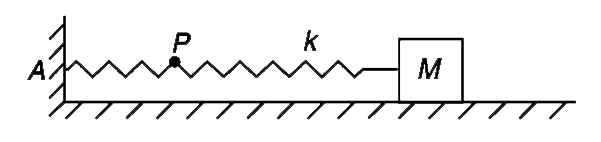
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
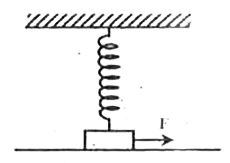
View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the plank , and between the cylinder and the ground. Find the time period of small oscillation of the system.

View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
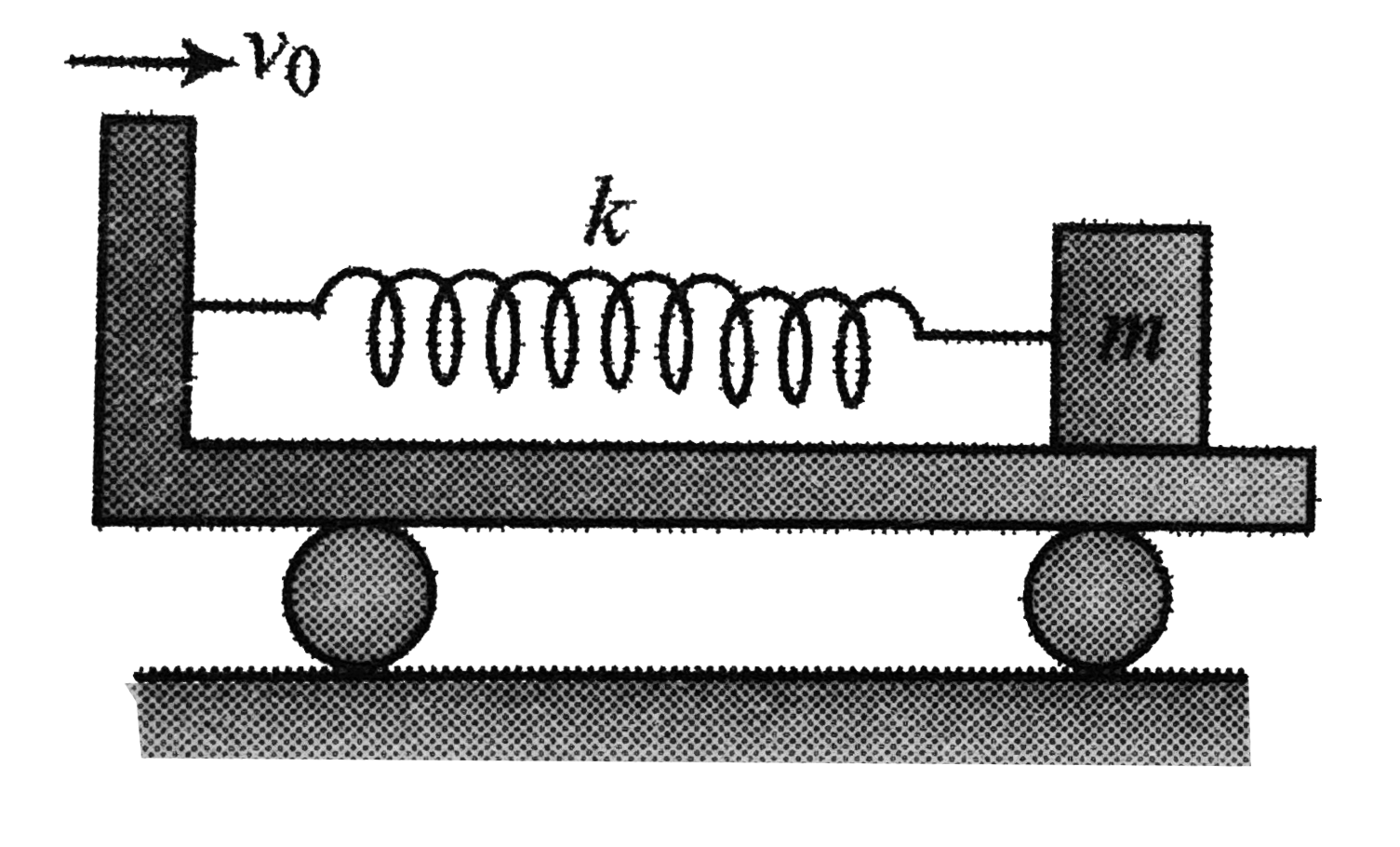
View SolutionA block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
View Solution

