Two bodies A and B of each of mass 100gm are allowed to move along a frictionless typical path as shown below. In order to have the same kinetic energy for the both the bodies at M, the initial velocity that should be given to B, if A starts from rest is
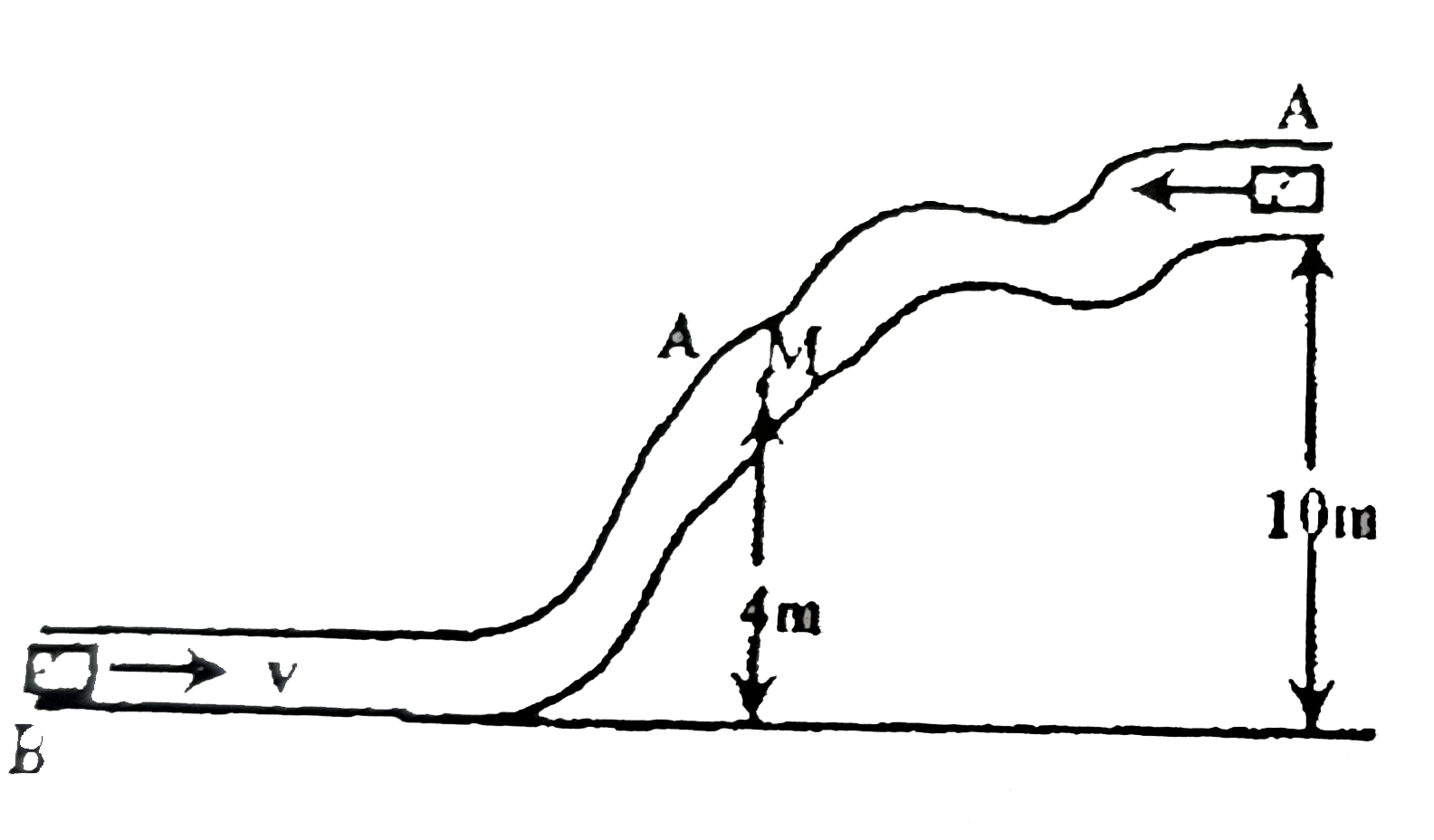
10m/s
√2m/s
11m/s
10√2m/s
(KEA) at M=mg(10−4)=6J
(KEa) at M=6J and (PEB) at M=110×10×4=4J
⇒(12mv2B)on ground=(TEB)M=(6+4)J
⇒v=√200=10√2m/s
Topper's Solved these Questions
Similar Questions
Two bodies of masses m1 and m2 have equal KE. Their momenta is in the ratio
View SolutionTwo bodies A and B each of mass m are fixed together by a massless spring . A force F acts on the mass B as shown in fig .3 (a)18. At the instant shown , the body A has an acceleration a What is the acceleration of B ?

View Solution
Knowledge Check
Two bodies A and B having masses in the ratio of 3 : 1 possess the same kinetic energy. The ratio of their linear momenta is then
A3:1B9:1C1:1D√3:1Two bodies A and B having masses in the ratio of 3 : 1 possess the same kinetic energy. The ratio of their linear momenta is then
A3:1B9:1C1:1D√3:1If a lighter body (mass M1 and velocity V1 ) and a heavier body (mass M2 and velocity V2) have the same kinetic energy, then-
AM2V2<M1V1BM2V2=M1V1CM2V1=M1V2DM2V2>M1V1
Two blocks A and B each having a mass of 20kg, rest on frictionless surfaces as shown in the figure below.Assuming the puelleys to be light and frictionless, compute :
(a) the time required for block A, to move down by 2m on the plane, starting from rest,
( b) tension in the string, connecting the blocks.
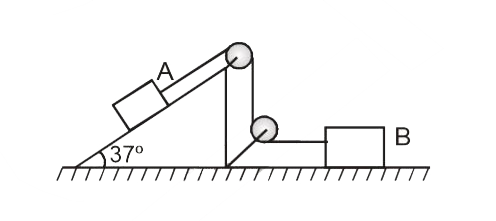
View SolutionThe kinetic energy acquired by a body of mass m in travelling a certain distance starting from rest, under a constant force is
View SolutionIf a lighter body (mass M1 and velocity V1 ) and a heavier body (mass M2 and velocity V2) have the same kinetic energy, then-
View SolutionTwo bodies A and B having masses in the ratio 3:1, possesses the same kinetic energy. The ratio of their linear momentum is
View SolutionTwo moving bodies having mass in the ratio 1 : 2 and kinetic energy in the ratio 1:8. Find the ratio of their velocities.
View Solution

