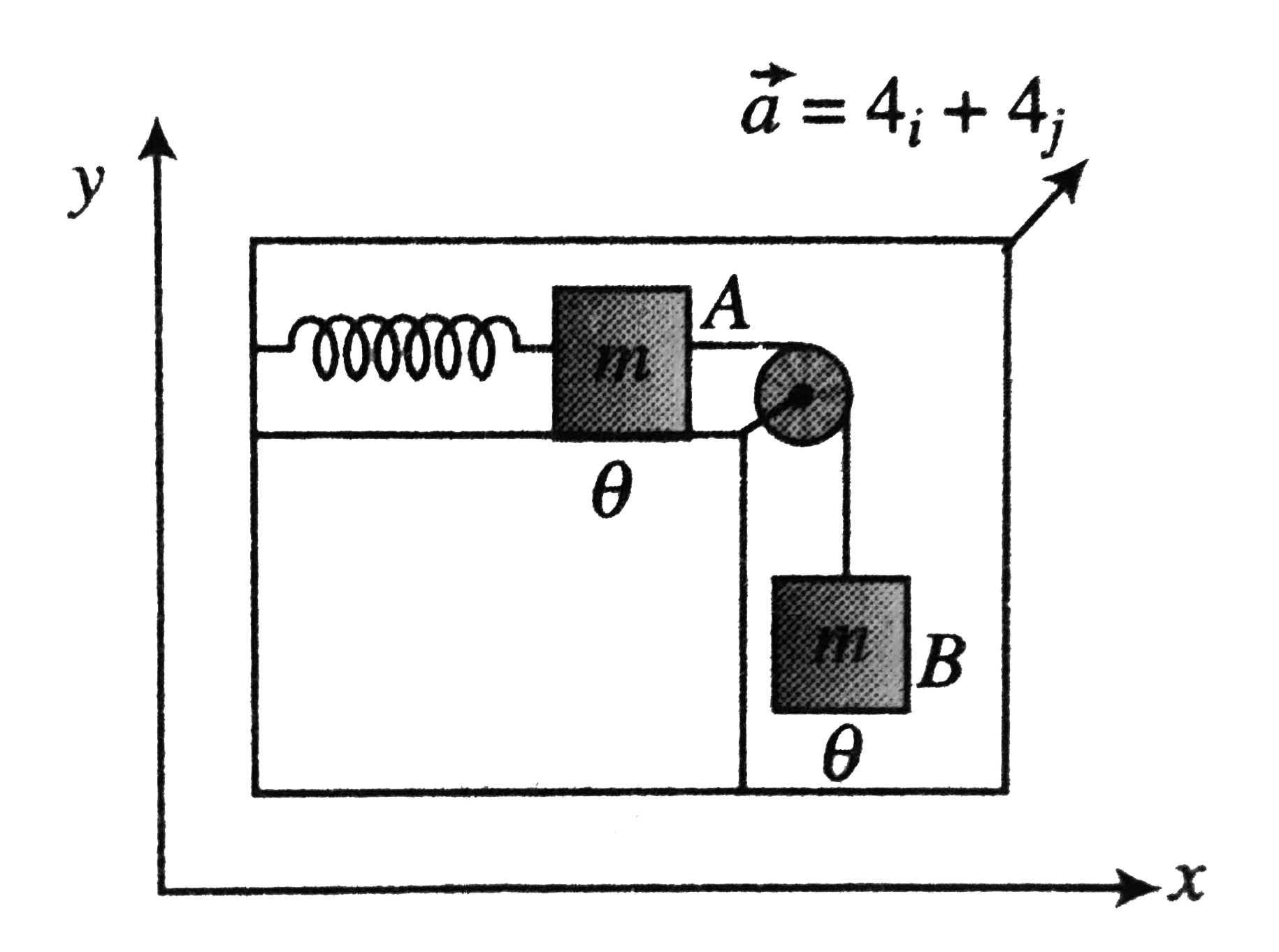
The arrangement shown in the diagram is moving in space with an acceleration a=4(ˆi+ˆj)m/s2. An ideal spring of natural length l0 having spring constant k=50N/m, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. Mass of each block A and B is equal to m=2kg.
(a) Calculate the minimum value of coefficient of friction so that spring remains in its natural length. (b) If μ is reduced to (9/35)th of the original value, calculate the maximum extension of the spring.
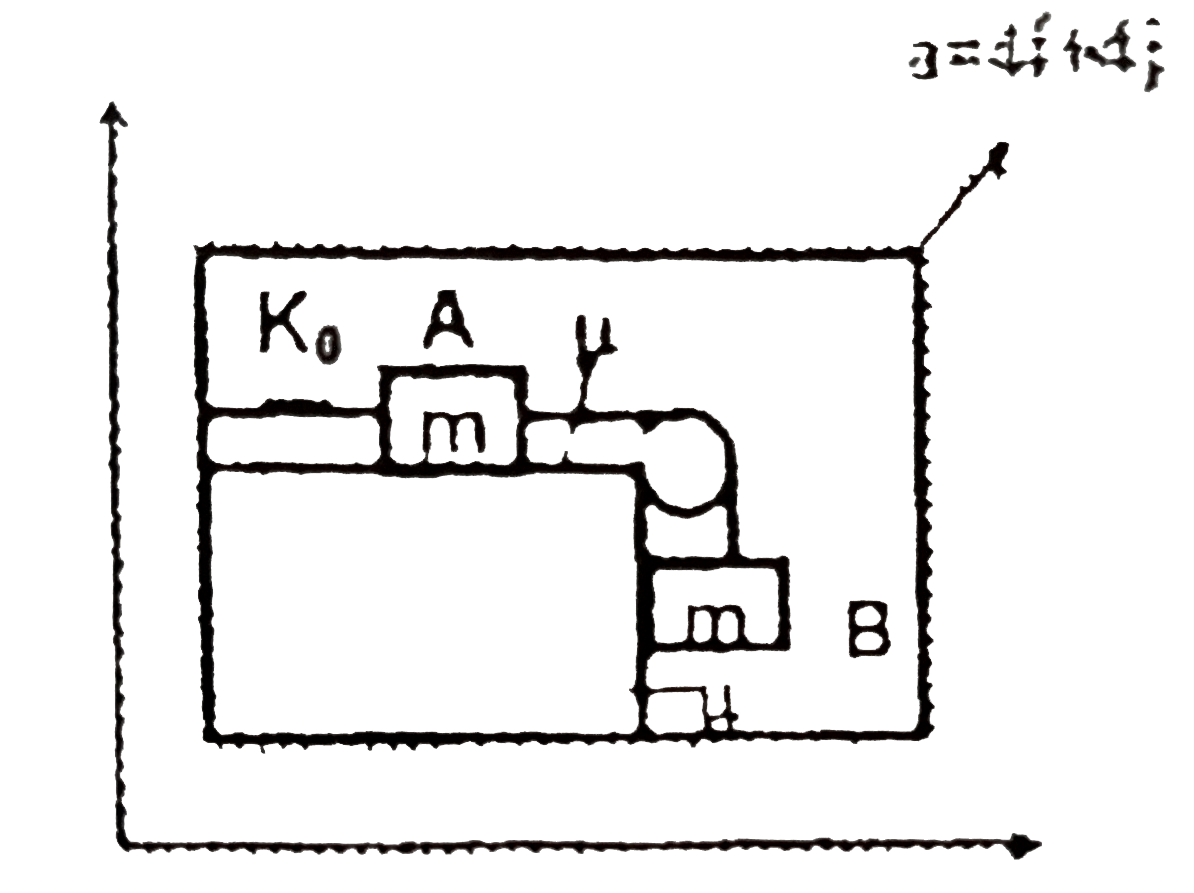
Case I : a=(4ˆi+4ˆj)m/s2, ax=4m/s2, ay=4m/s2
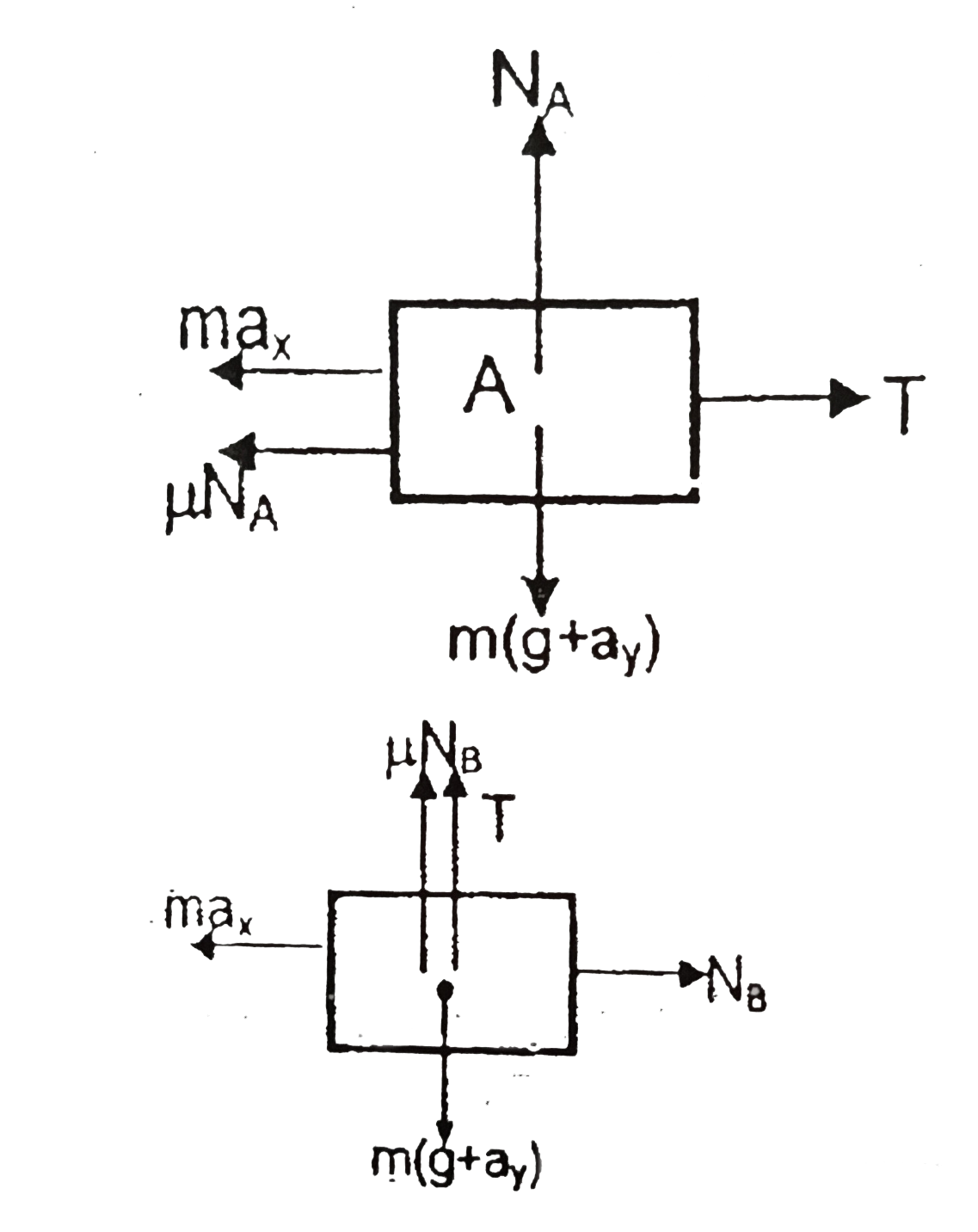
FBD of blocks A and B
NA=m(g+ay)=28N
T=max+μNA=8+28μ…..(1)
NB=max=8N
T+μNB=m(g+ay)
T+8μ=28…..(2)
From Eqs.(1) and (2), μmin=5/9
Case II : Let extension of spring =x, μ'=(5/9)×(9/35)=1/7
From work energy theorem :
mgx−μ'NAx−μ'NBx−maxx+mayx=1/2kx2
20x−(1/7)x×(28x)−(1/7)x×(8x)=25x2
x=0.6m
Topper's Solved these Questions
Similar Questions
The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in (cm) of the spring. (g=10ms−2).
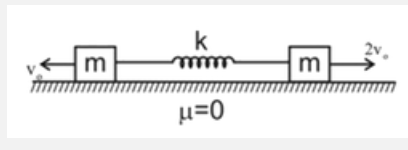
View SolutionThe figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
View Solution
Knowledge Check
Two blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
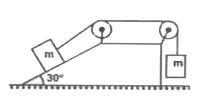 Ag/2Bg/4C2g/3D3g/4
Ag/2Bg/4C2g/3D3g/4Two blocks A and B are connected by as string as shown in figure. Friction coefficient of the incline plane and block is 0.5. The mass of the block A is 5kg. If minimum & maximum values of masses of the block B for which the block remains in equilibrium are m1 & m2 then find value of (m2−m1).
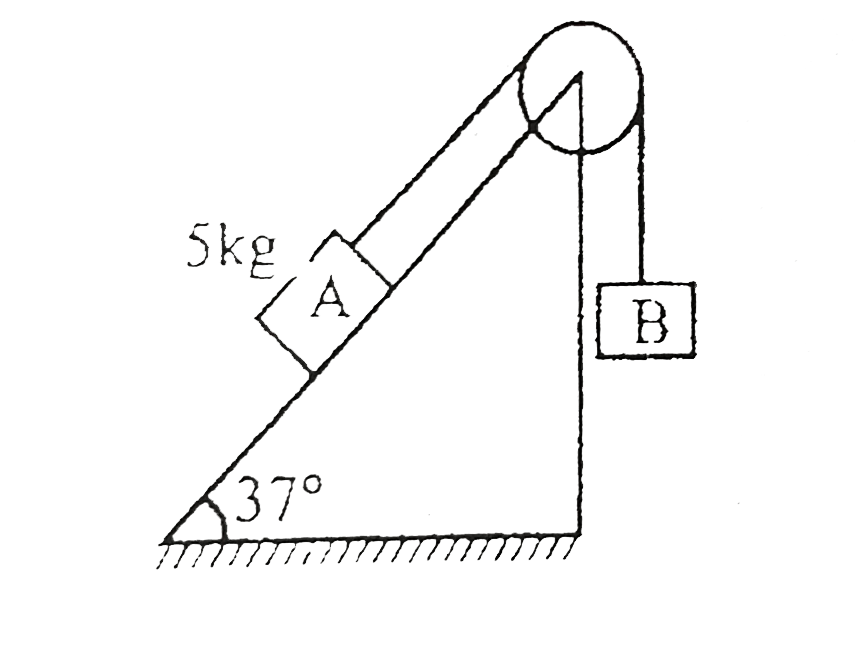 A4B6C3D2
A4B6C3D2Two block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
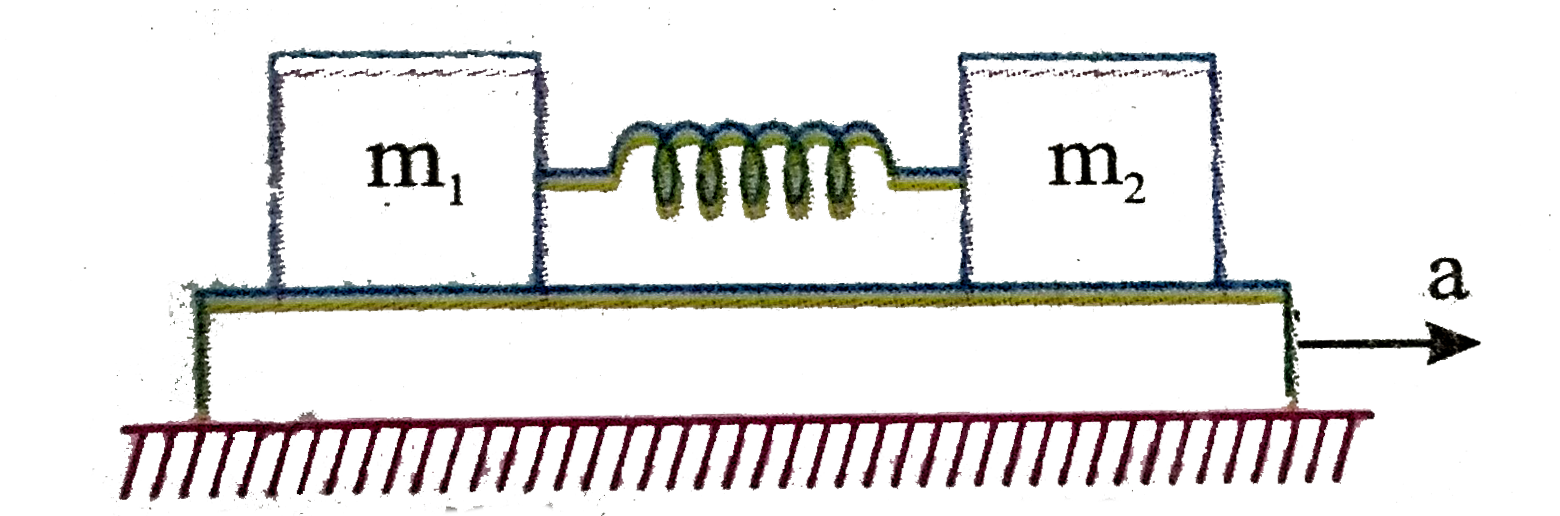 Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Four blocks are connected with a.string passing over a frictionless pulley fixed at the corner of a table as shown in figure. The coefficient of static friction of A with table is 0.50. The minimum mass m of the block, so that blocks do not move should be ...... kg.
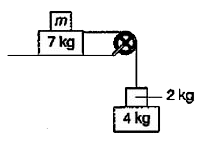
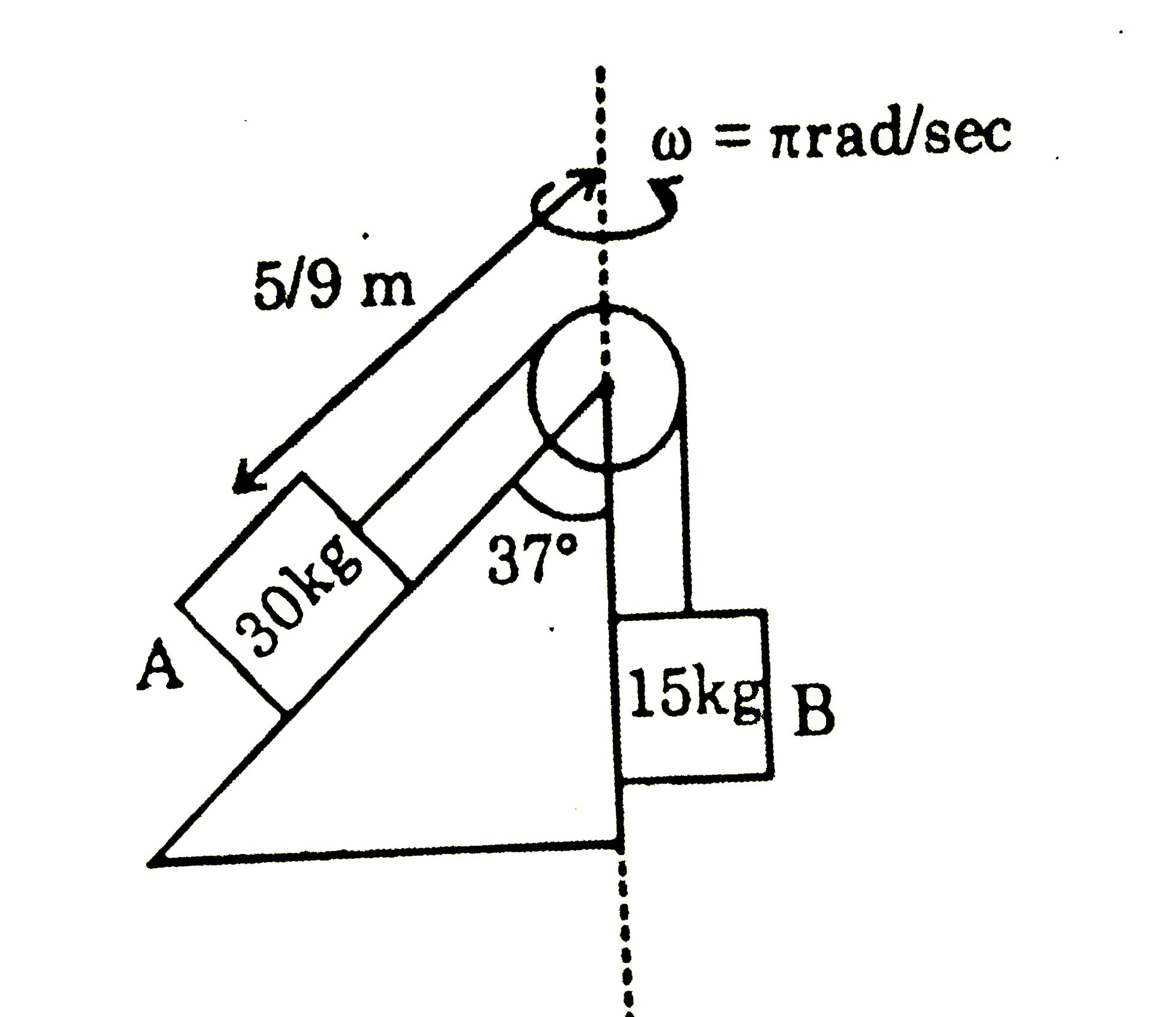
View SolutionTwo small blocks of mass mA=30 kg & mB =15 kg are connected with spring & kept on the wedge which is rotating about given axis as shown in figure. If blocks B remain in rest then minimum value of coefficient of friction between block A & wedge is μ0, then the value of μ20 is :
View SolutionTwo blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
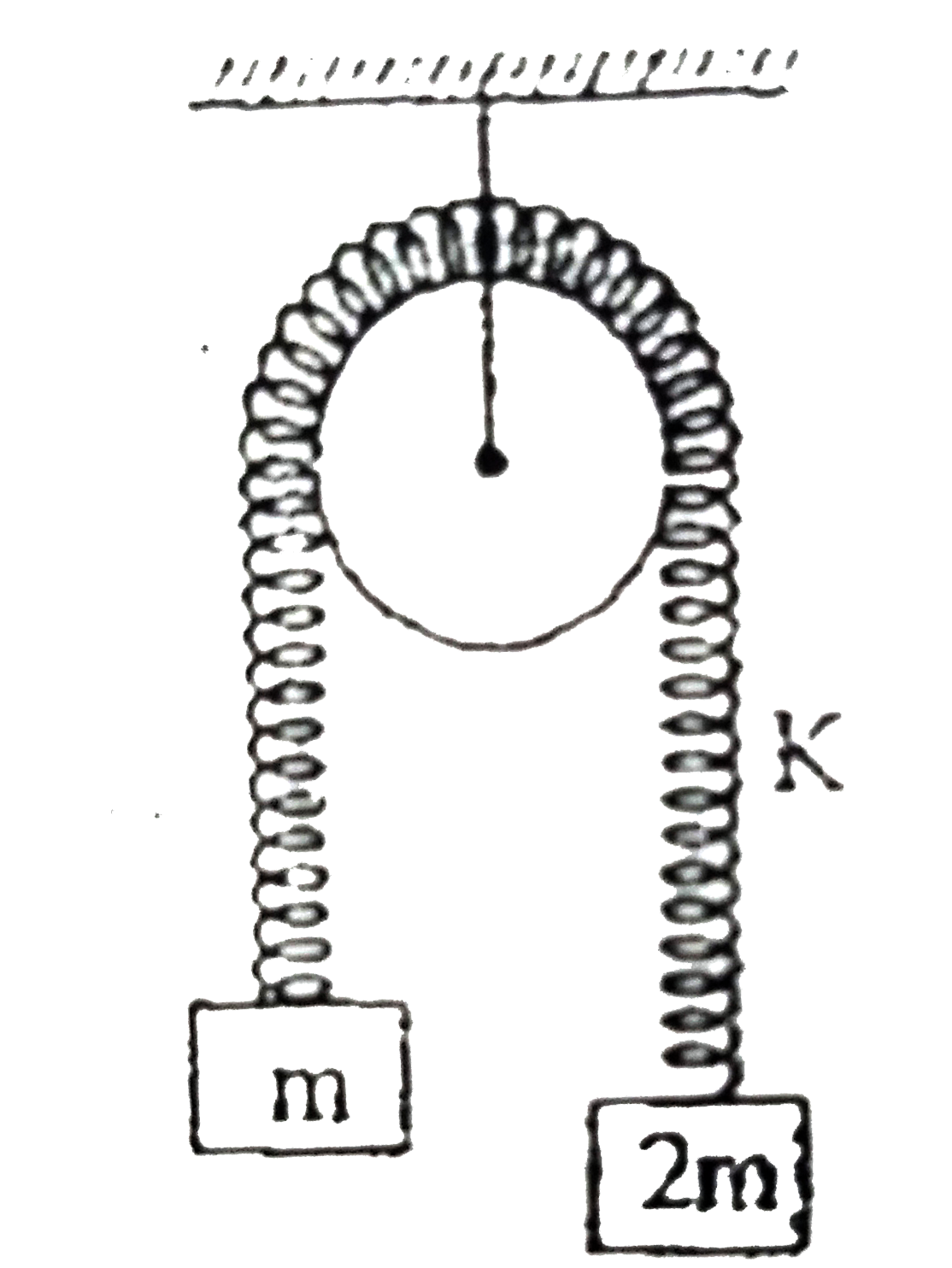
View SolutionTwo blocks of mass m and 2m are connected to a spring and wrapped around a smooth pulley as shown in the figure. Blocks are released together with spring in natural length. Calculate the maximum elongation (in meter) of the spring. Given mgK=3 meter.
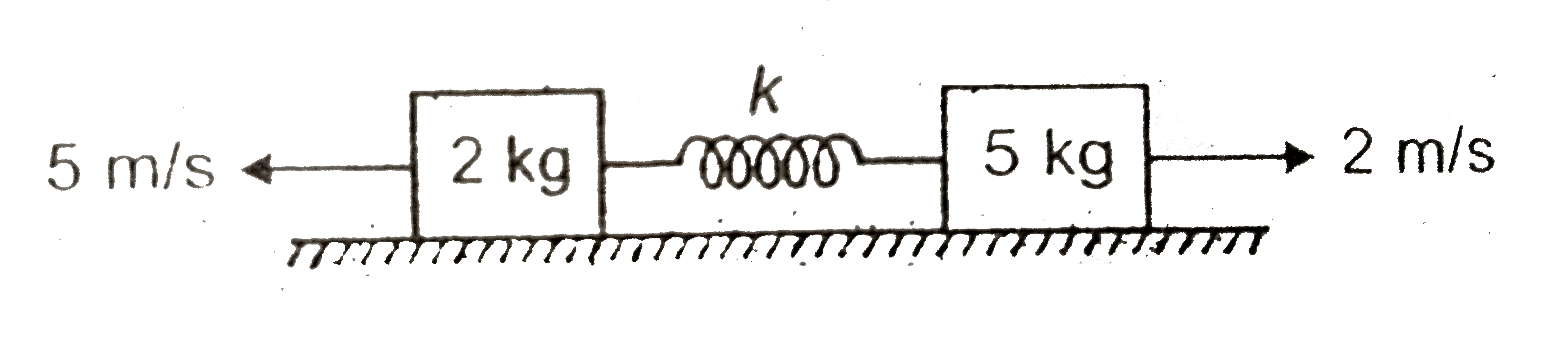
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View Solution

