A solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g=10m/s2)

Let the volume of the cylinder be V
When the cylinder is floating
upthrust =weight.
ρ(34V)g=mg, V=4m3ρ
Let the acceleration of the particle vessel be A(upwards)
In the reference frame of vessel, the acceleration of the cylinder is A/3.
∴mg+mA−unthrust=m(A/3)
mg+mA−ρVg'=m(A/3)
[Where g'=g+A= effective value of g for upthrust]
mg+mA−ρV(g+A)=m(A/3)
mg−43m(g+A)=−m23A
A=(−g/2) upwards
The acceleration of the vessel should be g/2 downwards.

Topper's Solved these Questions
Similar Questions
In the system shown in the adjoining figure, the acceleration of the 1 kg mass is m/s2. (take g=10m/s2)

View SolutionA wooden block is floating in a liquid, 50% of its volume is inside the liquid when the vessel is stationary. Percentage of volume immersed when the vessel moves upwards with an acceleration a=g2 is
View Solution
Knowledge Check
A block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
AVBV/2CarbitrayDzeroIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
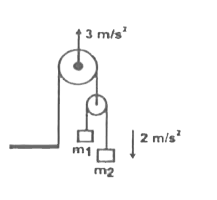 Awill be 8m/s2 upwardBwill be 4m/s2 upwardCwill be 14m/s2 upwardDThe value depends upon actual values of m1 and m2
Awill be 8m/s2 upwardBwill be 4m/s2 upwardCwill be 14m/s2 upwardDThe value depends upon actual values of m1 and m2A wooden block is floating in a liquid. About 50% of its volume is inside the liquid when the vessel is stationary, Percentage volume immersed when the vessel moves upwards with acceleration a=g.2 is
A75%B25%C50%D33.33%
Consider a solid cylinder of the density ρs cross section area A and h ploating in a liquid of density ρl as shown in figure (ρl>ρs) . It is depressed sligtly and allowed to oscillation.

View SolutionA solid cylinder of height h and mass m floats in a liquid of density ρ such that three fourth of its height is immersed. Now, the cylinder is released inside a liquid of density ρ4, contained in a downward accelerated vessel. Find the magnitude of acceleration of vessel A, for which cylinder sinks with relative acceleration of A3 w.r.t. vessel.
View SolutionA container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
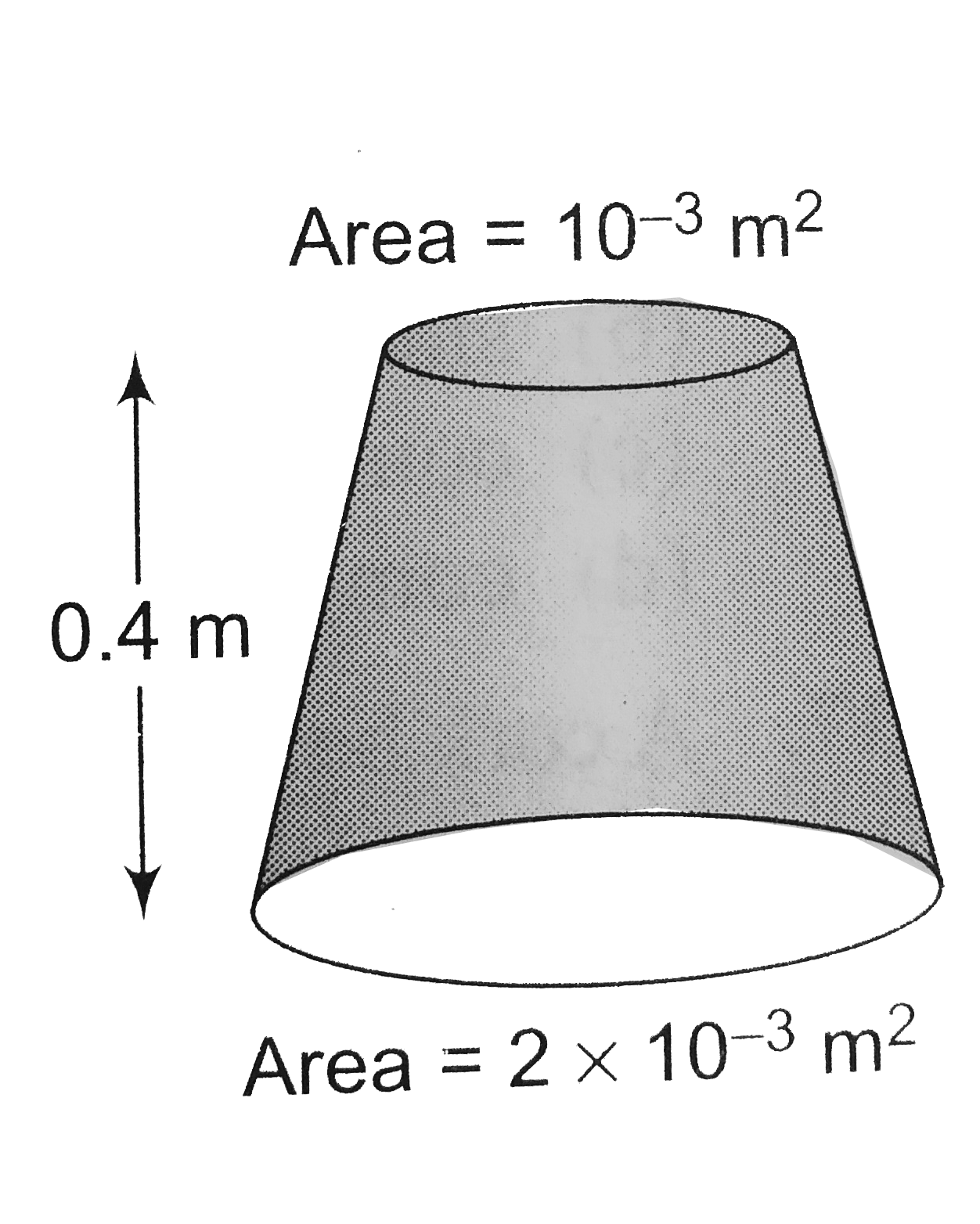
View SolutionA uniformly tapering vessel is filled with a liquid of density 900kg/m. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)(upper area=10−3m2,lower area=2×10−3m2)

View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
View Solution
