Consider a solid cylinder of the density ρs cross section area A and h ploating in a liquid of density ρl as shown in figure (ρl>ρs) . It is depressed sligtly and allowed to oscillation.

At equilibrium the net force on the cylinder is zero in the vertical direction.
Fnet=B−W=0,B= the buoyancy and W = the weight of the cylinder direction.
When the cylinder is depresed slightly by x, the buoyancy increases from B→B+σB, where σB=|x|ρlAg
The equation of motion is, therefore.
ρ,Ahd2xdt2=−ρlgρsh
and the angular frequency, ω, is
ω=√gρlhρs
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Solved Example
Explore 15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Consider a solid cylinder of height h, density ρs, cross-sectional area A is floating in a liquid of density ρl. The frequency of vertical oscillations was found to be gahbρci,ρds when depressed slightly and released. Then what is the value of a2bcd ?
View SolutionA solid cylinder of denisty ρ0, cross-section area A and length l floats in a liquid ρ(>ρ0 with its axis vertical, as shown. If it is slightly displaced downward and released, the time period will be :

View Solution
Knowledge Check
An object with uniform density ρ is attached to a spring that is known to stretch linearly with applied force as shown below.
When the spring-object system is immersed in a liquid of density ρ1 as shown in the figure, the spring stretches by an amount x1(ρ>ρ1). When the experiment is repeated in a liquid of density ρ2>ρ1, the spring stretches by an amount x2. Neglecting any buoyant force on the spring, the density of the object is
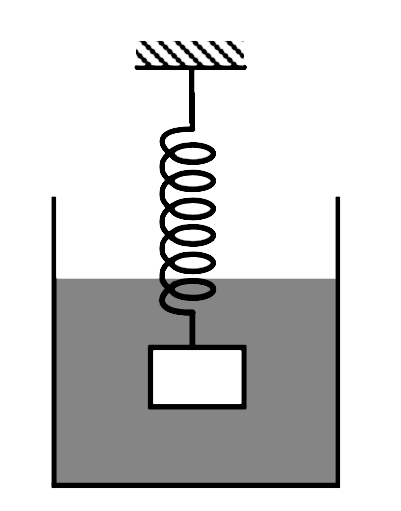 Aρ=ρ1x1−ρ2x2x1−x2Bρ=ρ1x2−ρ2x1x2−x1Cρ=ρ1x2+ρ2x1x2+x1Dρ=ρ1x2+ρ2x1x1+x2
Aρ=ρ1x1−ρ2x2x1−x2Bρ=ρ1x2−ρ2x1x2−x1Cρ=ρ1x2+ρ2x1x2+x1Dρ=ρ1x2+ρ2x1x1+x2The speed of transverse waves in a wire of length L , density ρ, cross - sectional area A and stretched with a tension T is given by
A√TLρAB√TAρC√TρLD√TρAL
A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionA stream line body with relative density ρ1 falls into air from a height h1 on the surface of a liquid of realtive density ρ2, where ρ2>ρ1. Find the time of immersion of the body into the liquid.
View SolutionA body of density ρfloats with a volume V1 of its total volume V immersed in one liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2, where ρ1>ρ2. Find the relative volumes immersed in two liquids.
View SolutionA body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionA ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.

View Solution

