A uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is and the coefficient of friction between the plank and cylender is . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
When the plank is situated symmeetrically on the drums, the reations on the plank from the droms will be equal and so the force of friction will be equal in magnitude but opposite in direction and hence, the plank will be equilibrium along vertical as well as horizontal direction.

Now if plank is displacement by x to the right the reaction will not be equal. For vertical equilibrium of the plank.
(i)
And for rotational of plank, taking moment about center of mass, we have
(ii)
Solving Eqs. (i) and (ii), we get
and
Now as R, so friction at B will be more than that at A and will bring the back, i.e. restoring force here is
As the restoring force is linear, the motion will be simple harmonic motion with force constant
So
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.2
Explore 23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA plank rests symmetrically on two cylinders which are separated by a distance of 2l and rotate with uniform speed in opposite direction. If the plank is displaced a little and then released, show that the motion of the plank is simple harmonic. Calculate the period of oscillations of the peak. The co-efficient of friction between the plank and either cylinder is μ.
View Solution
Knowledge Check
The friction coefficient between the plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then :
 Afriction force between plank and surface is 2μmg1+μBfrictional force on man is zeroCtension in the string is 2μmg1+μDnet force on man is zero
Afriction force between plank and surface is 2μmg1+μBfrictional force on man is zeroCtension in the string is 2μmg1+μDnet force on man is zeroA uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgThe friction coefficient between plank and flooe is μ. The man applies, the maximum possible foce on the string and the system remains at rest. Then
 Africtional force between plank and surface is 2μmg1+μBfrcitional force on man is zeroCtension is the string is 2μmg1+μDnet force on man is zero
Africtional force between plank and surface is 2μmg1+μBfrcitional force on man is zeroCtension is the string is 2μmg1+μDnet force on man is zero
A plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View SolutionA uniform plate of mass M stays horizontally symmetrically on two wheels rotating in opposite directions. The separation between the wheels is L. the friction coefficient between each and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

View SolutionA uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.
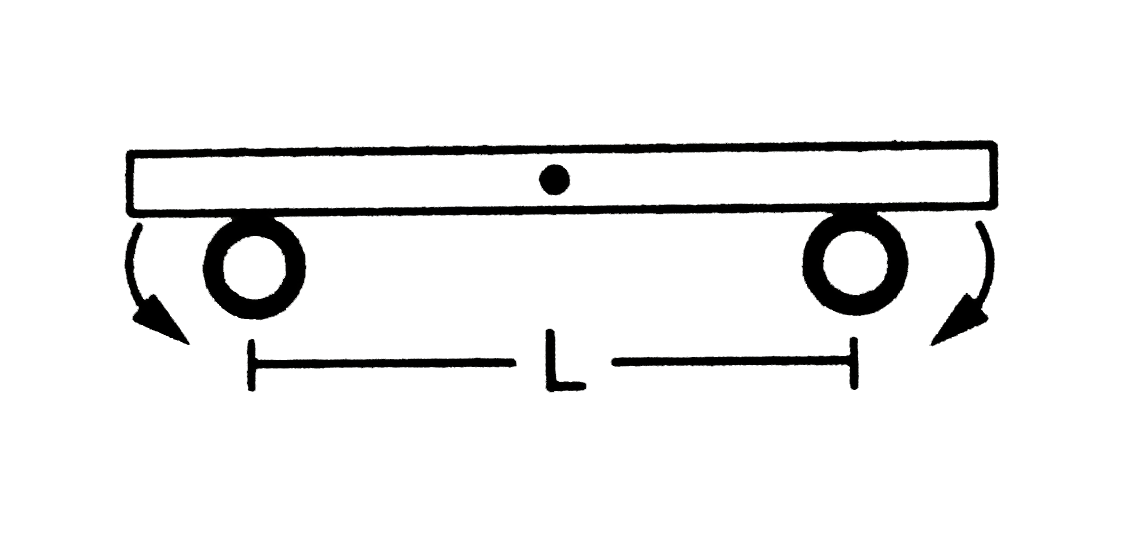
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
View Solution

