A circular spring of natural length l0 is cut and weided with two beads of masses m1andm2each that the such that the ratio of the original spring is k find the frequency of oscillation of the heads in a smooth horizontal rigid tube. Assume m_(1) = m and m_(2) = 3 m.

When m1 is displaced x, each spring will be deformedby same amoun. Hence, the springs are connected in parallel. The equivalent spring constant is
keq=k1+k2

If the spring is cut, the force constant of spring
k∝1l⇒k1l1=k2l2=kl
Substituting l1=l/5andl2=4/5, we have
k1=5kandk2=54k
Then keq=254k
Now we have two partical of masses m1andm2 and one spring of stiffness
keq=254k
The reduced mass is μ=m1m2(m1+m2)
where m1=mandm2=3m
This gives μ=3/4m
Substituting μ=3/4mandkeq=25/4k in the formula
ω=√keqμ⇒ω=
⎷254k34m=√25k3m=5√k3m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.2
Explore 23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution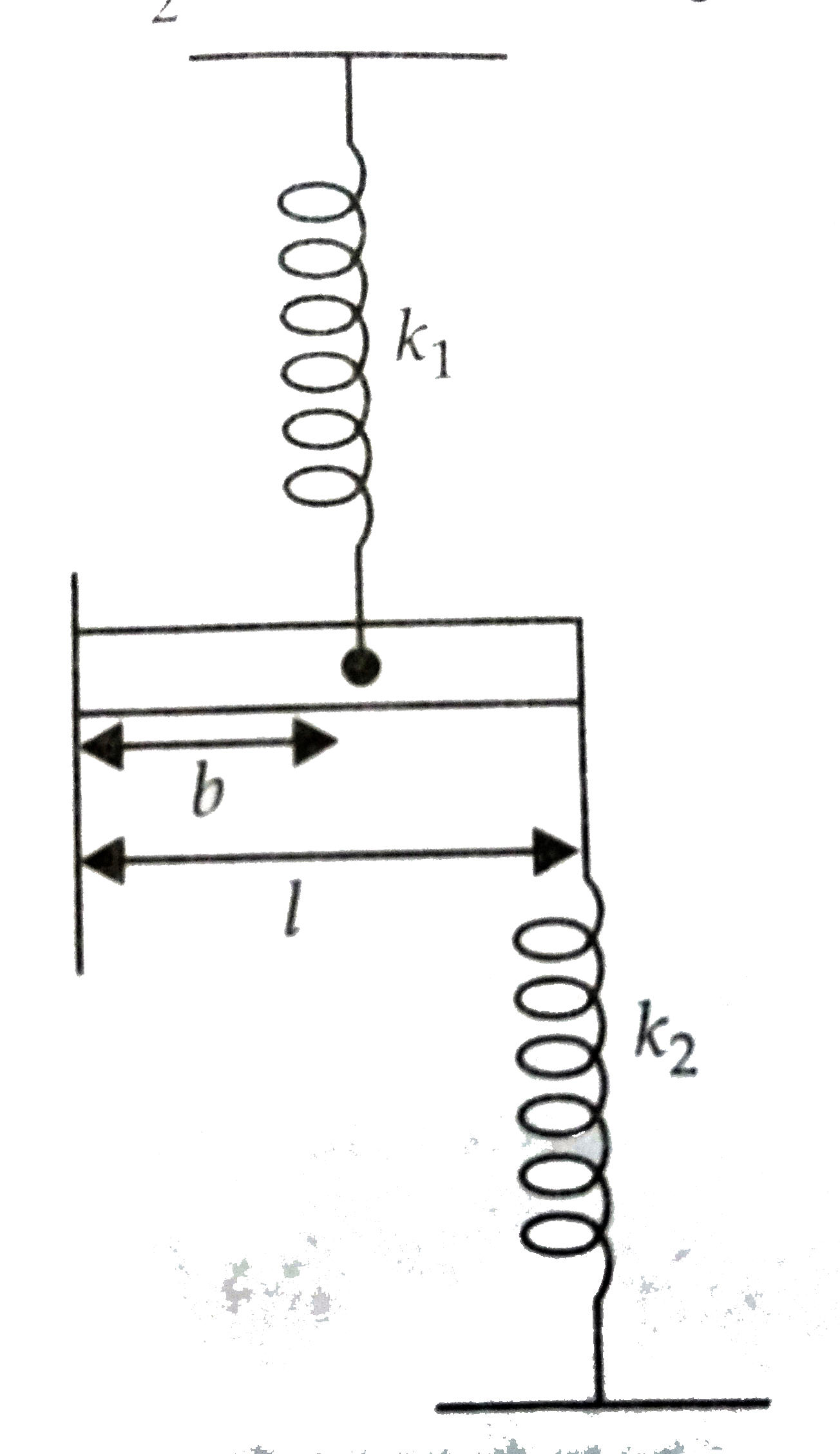
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
Knowledge Check
Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
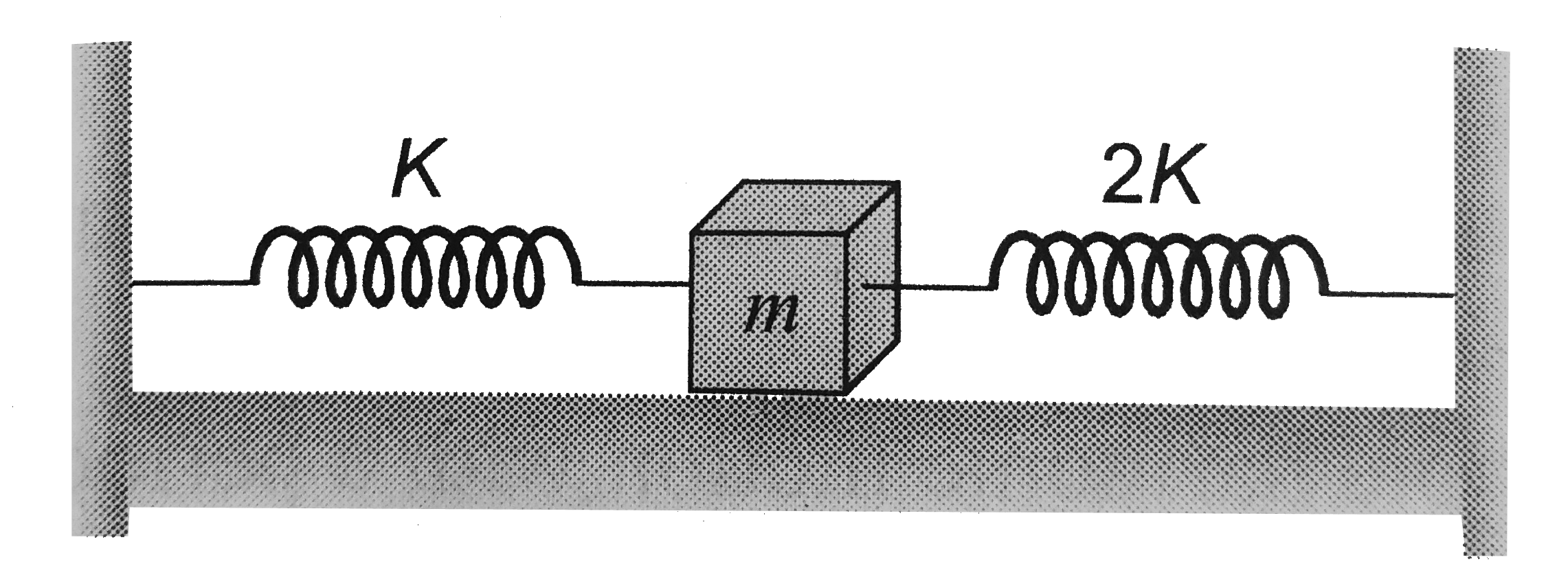 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)Two springs are joined and connected to mass m as shown. If the springs separately have force constants K1 and K2 , then frequency of oscillation of mass m is
 A12π√K1K2(K1+K2)mB2π√(K1+K2)mK1K2C2π√K1K2mD12π√mK1+K2
A12π√K1K2(K1+K2)mB2π√(K1+K2)mK1K2C2π√K1K2mD12π√mK1+K2
Two springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionA block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionA compound pendulum consists of a rigid light rod having two spherical bobs of masses m1andm2 at distance l1andl2 from the centre of suspension. Find the time period of oscillations of the pendulum
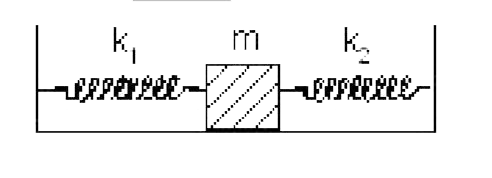
View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-
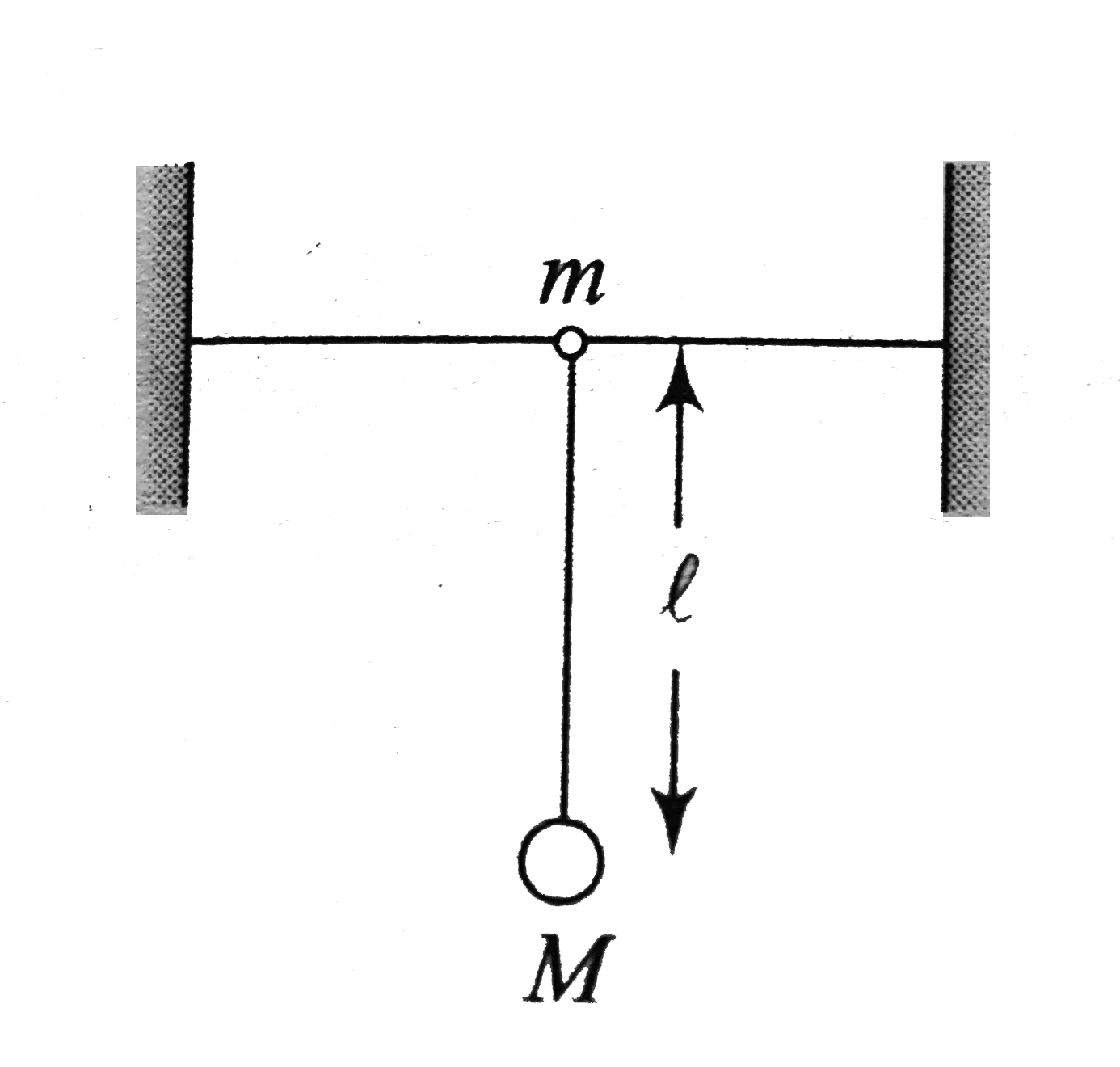
View SolutionA smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
View Solution

