Figure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards loft so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.

As shown in figure , as the block its released from rest at a distance 5/3 from its mean position, this will be the amplitude of oscillation. But on the other side of mean position block can move only up to a distance l from mean position and then it will return from this point with equal velocity due to elastic collision . Consider figure . If no right wall is present during oscillation, block P will excute complete SHM on right side of mean position also up t its amplitude 5l/3 . Thus, we can observe the block P at a point X at distance l from mean position (where in our case wall is present) . if block passes this position at speed v (which is the speed with , which block bites the wall in our case) after reaching its exterme position y, it willl return and during return path it will cross the position X with the same speed v (as displacement from mean position is same).

Thus, we can state that in our case of given problem , that block P is executing SHm but it skips a XYX on right half of its motion due to electric collision of the block with the wall. if T0 is the time period of this oscillation we look at figure which shown the corresponding circular motion repersantation. Here during oscillation of point P partical P0 covers its circular motion along ECDAF, and from F it instantly jumps to E (due to elastic collision of P with wall at X) and again carry out ECDAF and so on thus we can find the time of this total motion as

t=π+2θω=π+2sin−1(3/5)√km
=√mk[π+2sin−1(32)]
We can also find the time period of this motion by sub-tracting the time FYE from the total time period as
t=2π−2cos−1(35)ω
=√mk[π+2cos1(35)]
Equations (i) and (ii) will result same numerical value.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.2
Explore 23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
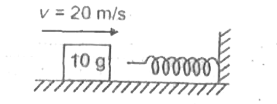 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43mIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
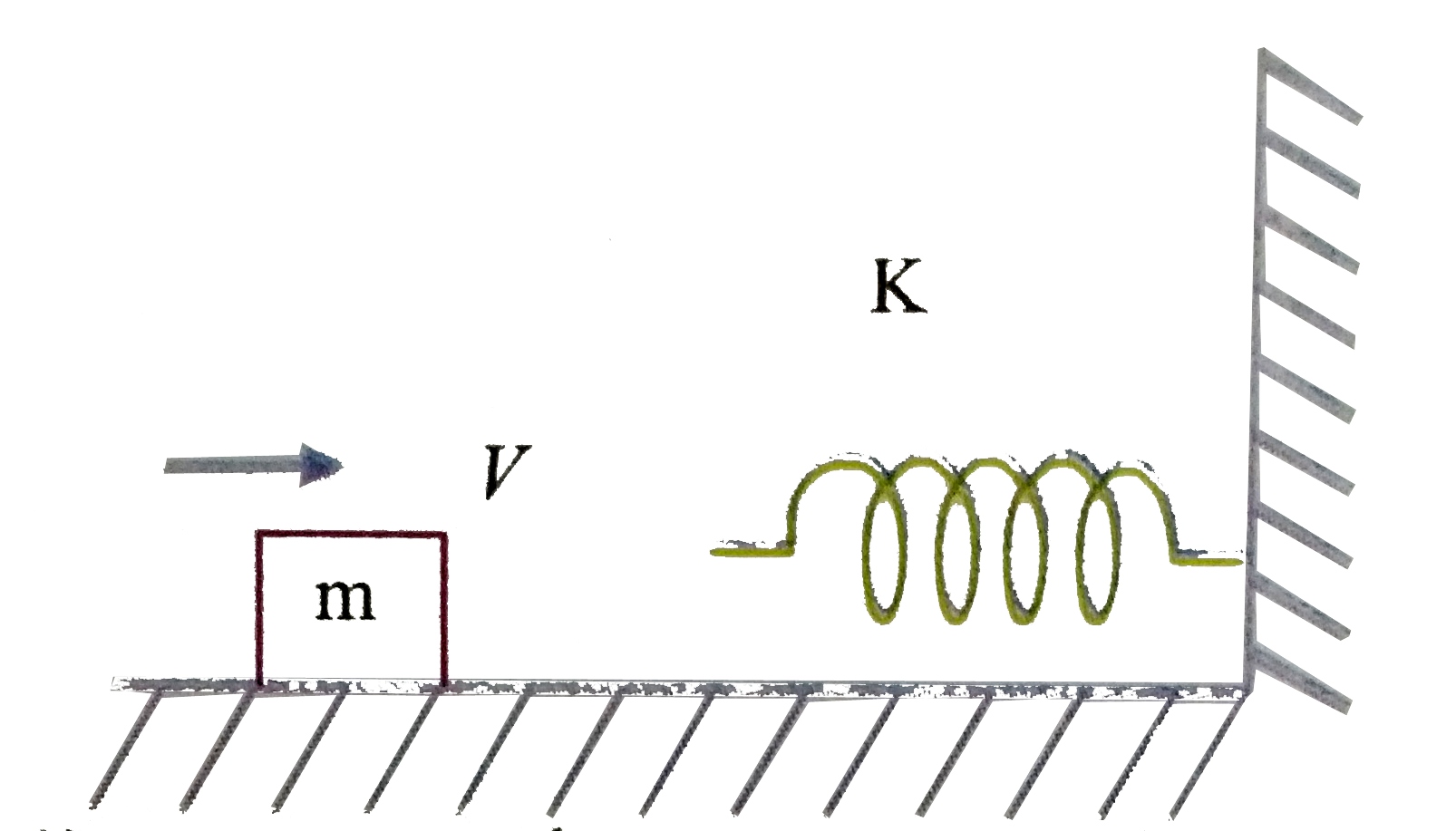
A block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m=25kg on a smooth horizontal surface with a velocity →v=3ms−1 meets the spring of spring constant k=100N/m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are.
 .
.
View SolutionA block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to

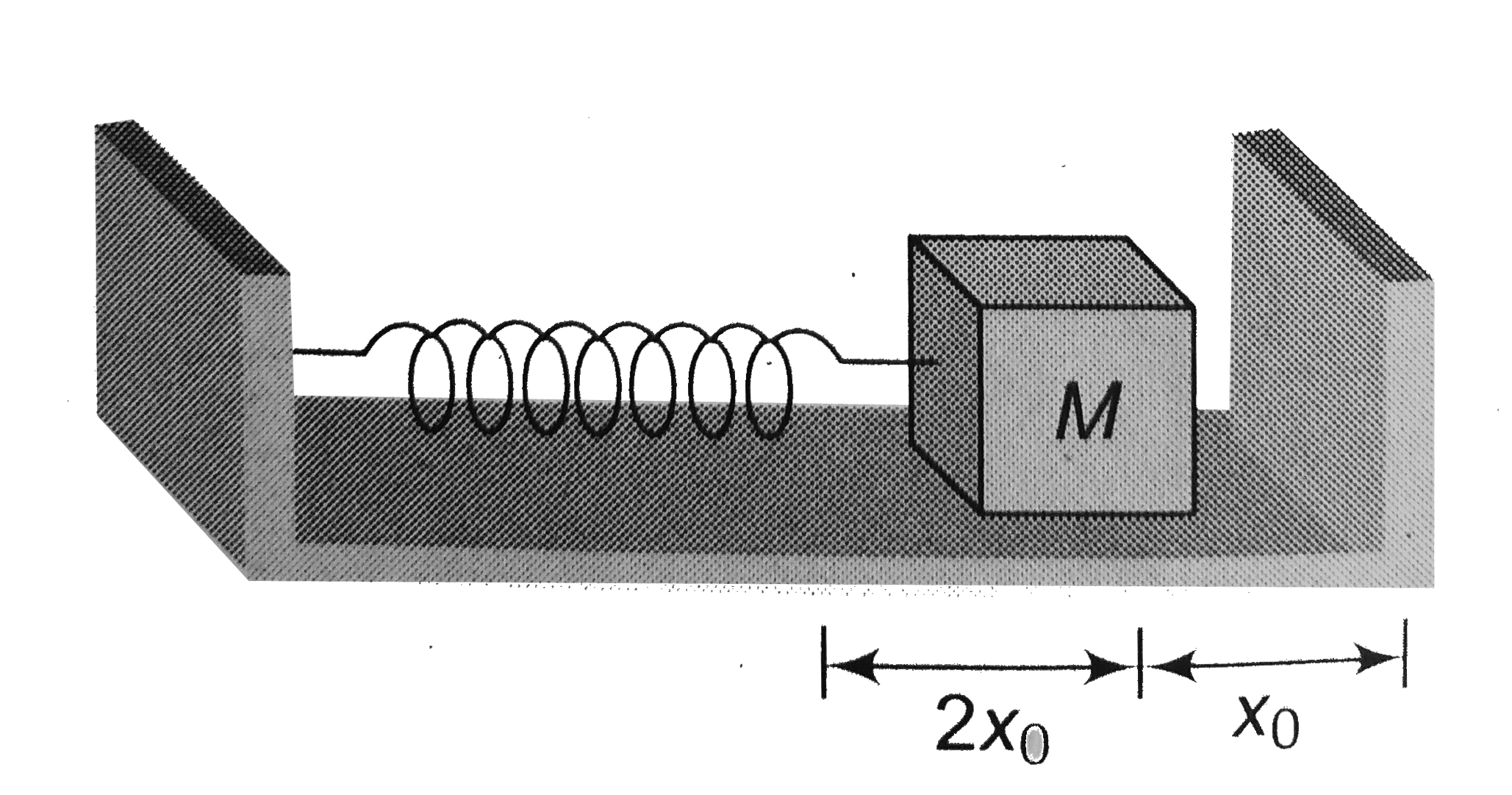
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface There is another and wall at a distance x0 from the block The spring is then compressed by 2x0 and released The time taken to at the wall is
View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
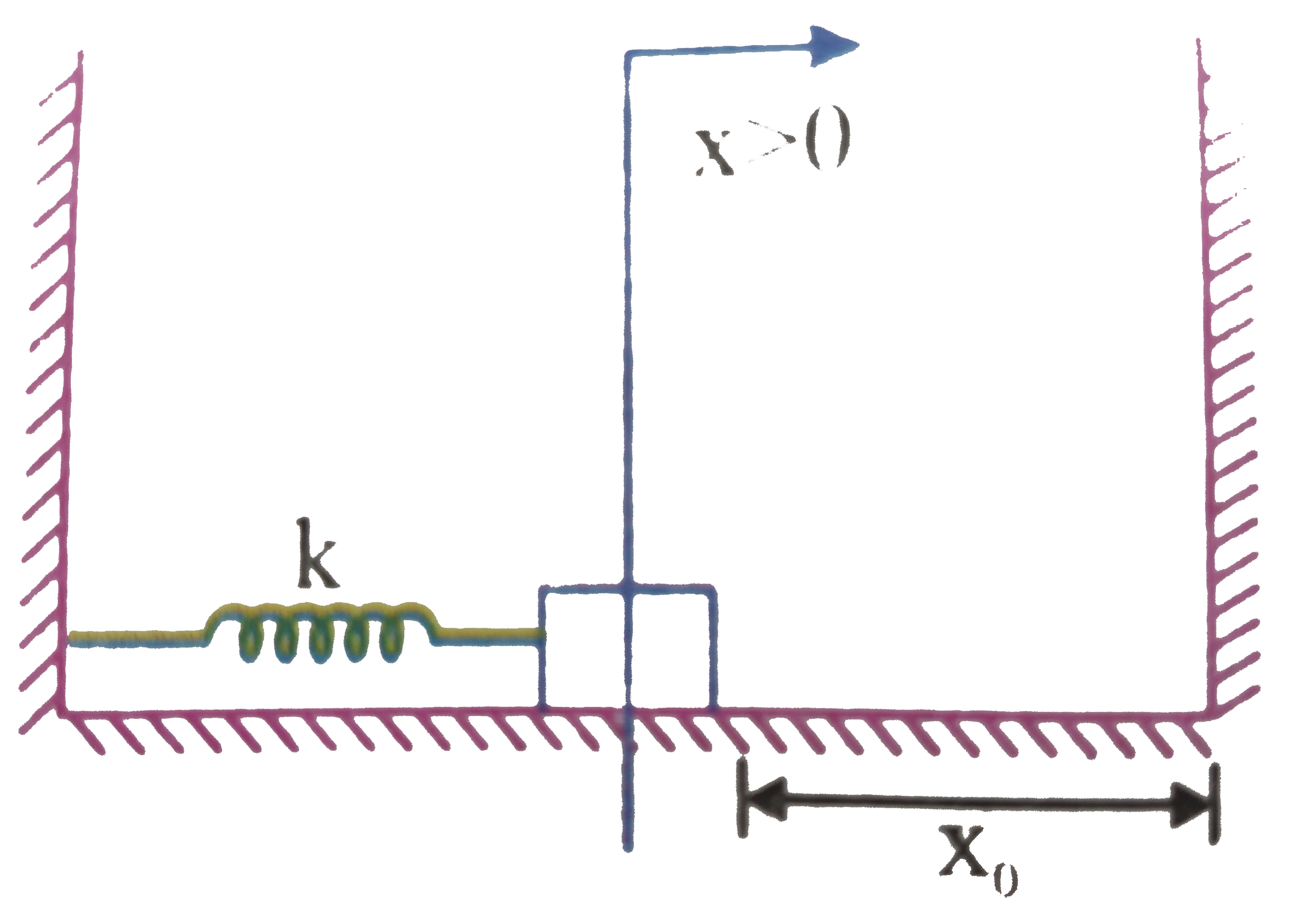
Find the time period of motion of the block:
View Solution

