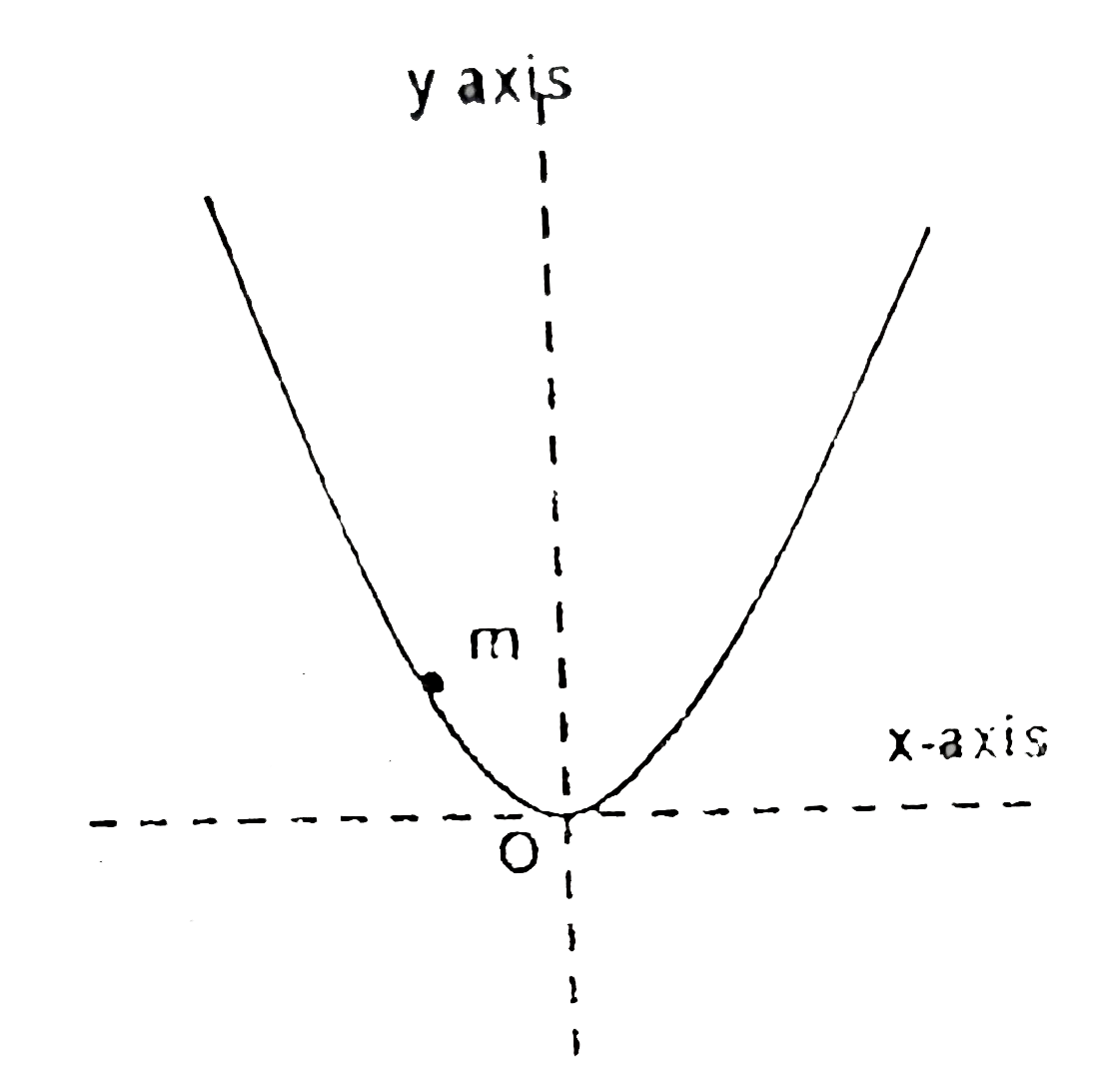
A point mass is displaced slightly from point and released. It is constrained to move along parabolic path having equation then its angular frequency of oscillation is :
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
A particle of mass 5×10−5kg is placed at the lowest point of a smooth parabola having the equation 20t2=y (x, y in m). Here y is the vertical height. If it is displaced slightly and it.is constrained to move along the parabola, find the angular frequency (in rad/s) of small oscillations.
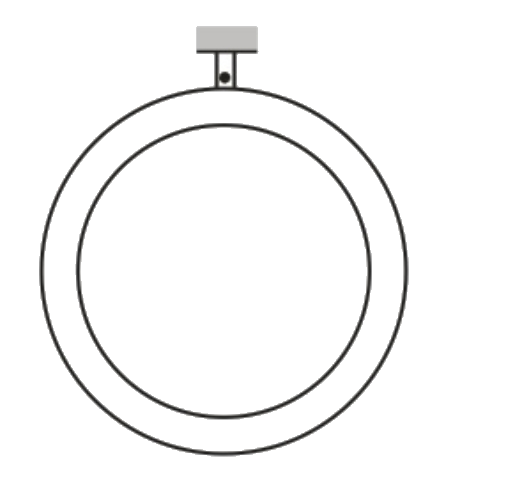
View SolutionA ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is
View Solution
Knowledge Check
A particle of mass m is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton x2=4ay. The angular frequency of small oscillation is given by
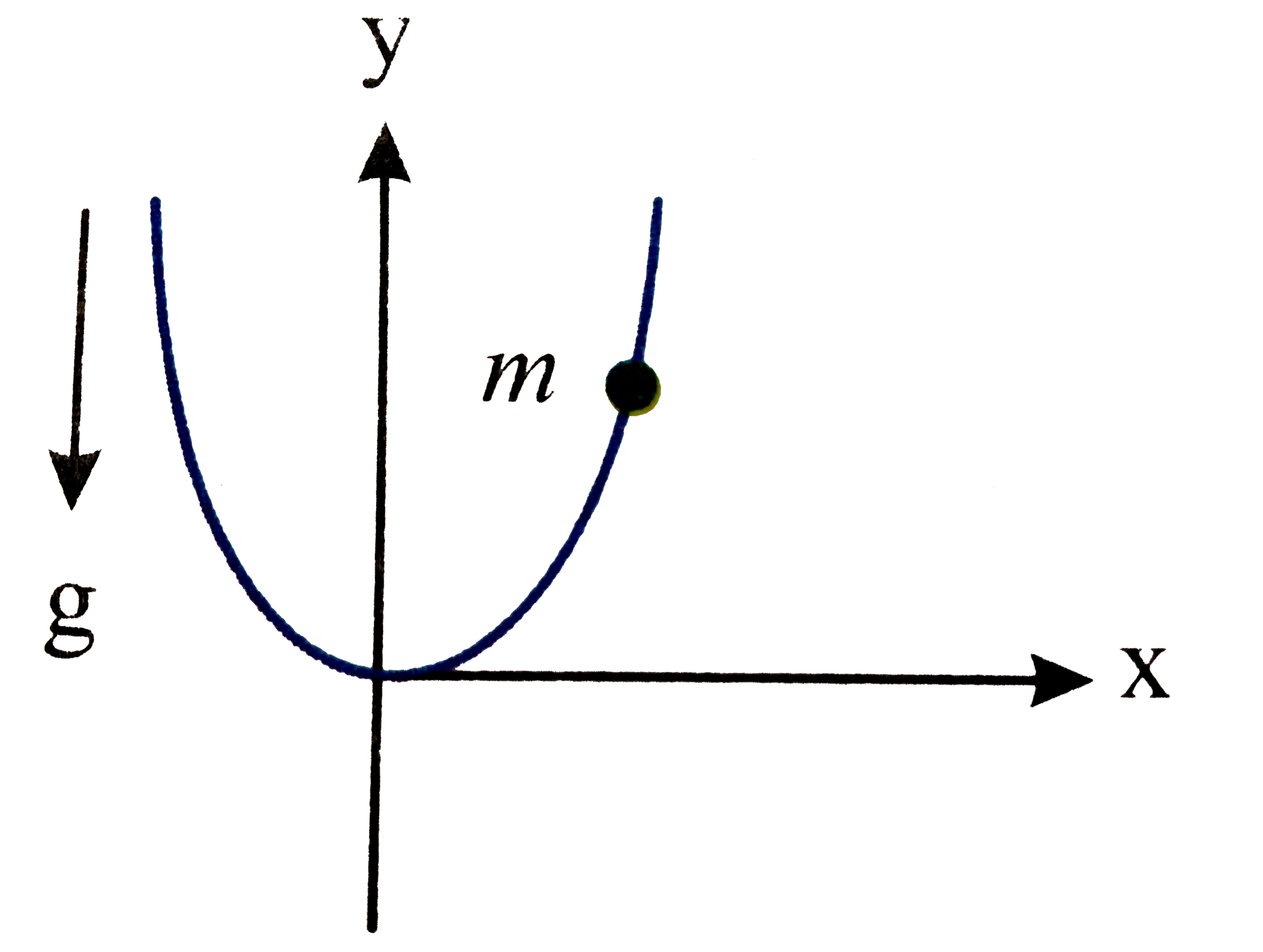 A√ghB√2ghC√(g2a)D√(ga)
A√ghB√2ghC√(g2a)D√(ga)A pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
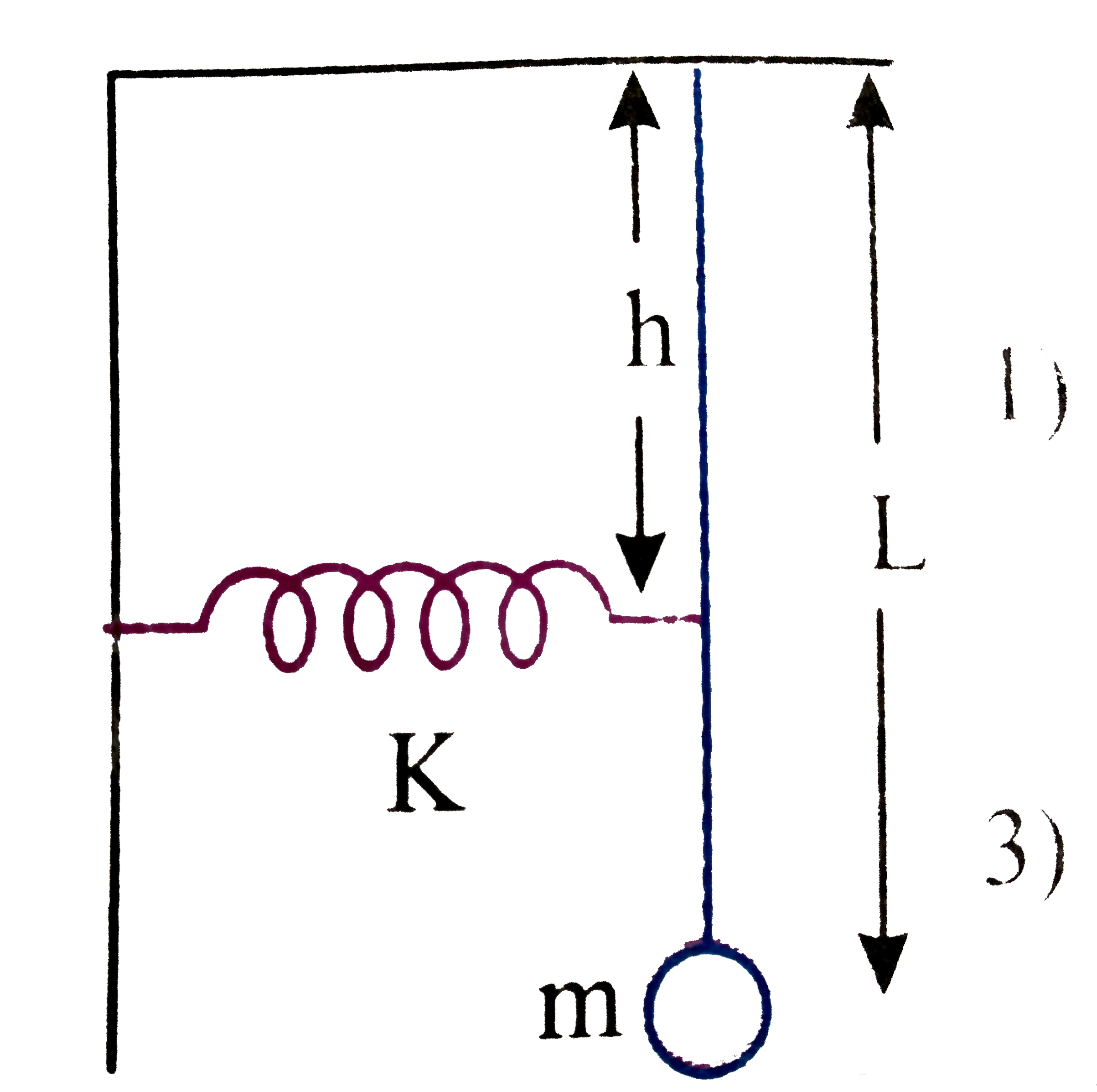 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2If at some instant of time, the displacement of a simple harmonic oscillator is 0.02 m and its acceleration is 2ms−2, then the angular frequency of the oscillator is
A100 rad s−1B10 rad s−1C1 rad s−1D0.1 rad s−1
A small point mass m has a charge q, which is constrained to move inside a narrow frictionless cylinder, At the bae of the cylinder is point mass of charge Q having the same sign as q. If the mass m is displaced by a small amount from its equilibrium position and released. it will exhibit simple harmonic motion. Find the angular frequency of the mass?

View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View SolutionOne end of a spring of negligible unstretched length and spring constant k is fixed at the origin (0,0) . A point particle of mass m carrying a positive charge q attached at its other end . The entire system is kept on a smooth horizontal surface . When a point dipole p pointing towards the charge q is fixed at the origin , the spring gets stretched to a length l and attains a new equilibrium positition (see figure below) . if the point mass is now displaced slightly by Δl<<l from its equilibrium position and released it is found to oscillate at frequency 1δ√km. The value of δ is ________.
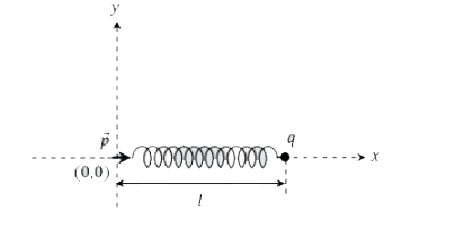
View SolutionA block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionThe acceleration of a particle in SHM is 0.8ms−2, when its displacement is 0.2m. The frequency of its oscillation is
View Solution