A certain amount of ice is supplied heat at a constant rate for 7 minutes. For the first one minute the temperature rises uniformly with time. Then, it remains constant for the next 4 minute and again the temperature rises at uniform rate for the last two minutes. Calculate the final temperature at the end of seven minutes.
(Given, L of ice =336×(103)J/kg and specific heat of water =4200J/kg.K).
The initial temperature of ice is −30∘C.
The final temperature at the end of 7 min is 40∘C.
The final temperature at the end of 7 min at 30∘C
Between t=1min to t=5min it does not changes its phase.
Let m be the mass of ice and q the rate by which heat is supplied, then
q×1=m(0.5)(−θi)…..(1)
q×4=m×80…..(2)
q×2=mI.θf…..(3)
From these equation
Qf=40∘C
Qi=−40∘C
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
Heat is supplied to a certain amount of ice at a constant rate for 9 min. For' the first 1 min, the temperature rises uniformly with time, Then the temperature remains constant for the next 5 min and after that again temperature rises at uniform rate for last 3min. If the ratio of magnitude of final temperature to initial temperature is P∘C, then find the 'value of 4P. (Given: S_ (ice )=0.5 (cal) (g)^(-1)/overset(o) \ C^(-1), L_(f)=80 (cal g).
View SolutionHeat is supplied to a ice at a constant rate Temperature variation with time is as shown in figure. Then –
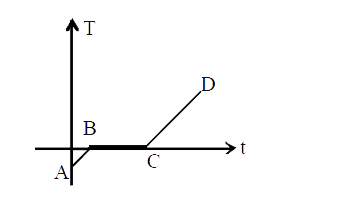
View Solution
Knowledge Check
A certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
Final temperature at the end of 7 min isA10∘CB20∘CC30∘CD40∘CA certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
The initial temperature of ice isA−10∘CB−20∘CC−30∘CD−40∘CA first − order reaction is 20% complete in 10 minutes. Calculate the rate constant of the reaction.
A0.223min−1B0.0322min−1C1.023min−1D0.123min−1
When a certain amount of heat is supplied to a diatomic gas at constant volume, rise in temperature is T0. When same heat is supplied to the gas at constant pressure, find the rise in temperature
View SolutionA metal ball cools from 62∘C to 50∘C in 10min and to 42∘C the next ten minutes. What will be its temperature at the end of next ten minutes ?
View SolutionA cyclist moves with a speed of 30km/hr in the first 10 minutes, with speed of 15km/hr in the next 20 minute and with a speed of 40km/hr in the last 15 minutes Calculate the average speed of the cyclist.
View SolutionHeat is being supplied at a constant rate to the sphere of ice which is melting at the rate of 0.1 gm/s. It melts completely in 100 s. The rate of rise of temperature thereafter will be
View SolutionA body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton's law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
View Solution

