In the figure shown surfaces are smooth and blocks A and B have same mass m. The two bodies are displaced right and released. It is found that bodies move according to the equation xA=Asin(ωt+ϕ), XB=2Asin(ωt+ϕ)

K1K2=32
K1K2=12
K1K2=1
K1K2=2
K2A=ω2(2A)
K1A−K2A=ω2A
⇒K2K1−K2=21
⇒K1K2=32
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
Knowledge Check
A particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
Awith amplitude x0/2Bwith amplitude 2x0Cwith the period 2xωDwith the period πωIn the figure shown A and B are free to move . All the surface are smooth. Mass of Aism. Then
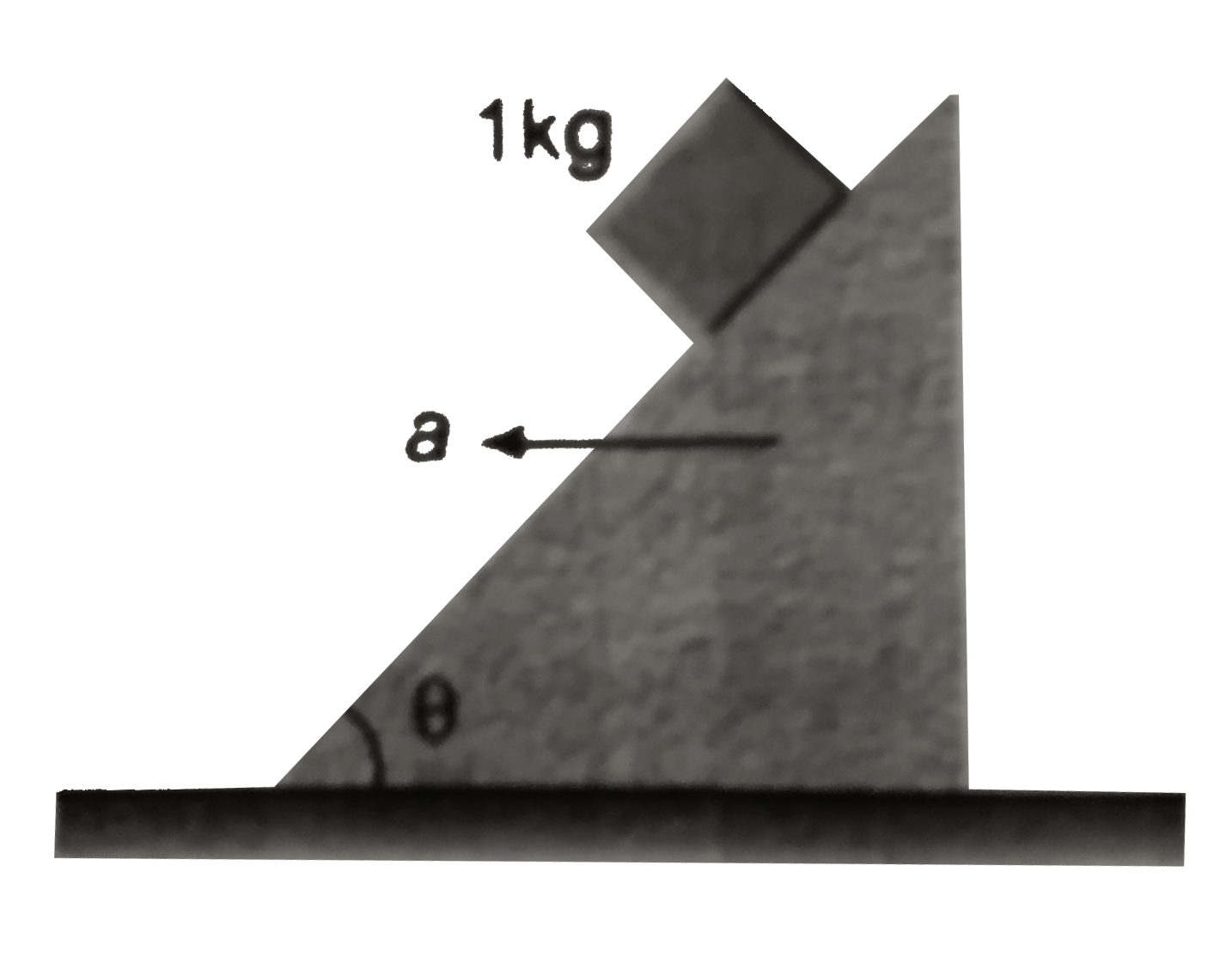 Athe acceleration of A will be more than gsinθBthe acceleration of A will be less than gsinθCnormal reation A due to B will be more than mgcosθDnormal reation A due to B will be less than mgcosθ
Athe acceleration of A will be more than gsinθBthe acceleration of A will be less than gsinθCnormal reation A due to B will be more than mgcosθDnormal reation A due to B will be less than mgcosθIn the figure shown all the surface are smooth. All the blocks A, B and C are movable, x-axis is horizontal and y-axis verticle as shown. Just after the system is released from the position as shown.
 AAcceleration of 'A' relative to ground is in negative y-directionBAcceleration of 'A' relative to B is in positive x-directionCThe horizontal acceleration of 'B' relative to ground is in negative x-directionDThe acceleration of 'C' relative to 'B' is directed along the inclined surface
AAcceleration of 'A' relative to ground is in negative y-directionBAcceleration of 'A' relative to B is in positive x-directionCThe horizontal acceleration of 'B' relative to ground is in negative x-directionDThe acceleration of 'C' relative to 'B' is directed along the inclined surface
Three sinusoidal displacements are applied in X-direction to a point mass in such a way that total displacement is zero and the mass comes to rest. What are the values of B and ϕ if the equations are
x1(t)=Asin2ωt
x2(t)=Asin(2ωt+4π3)
x3(t)=Bsin(2ωt+ϕ)
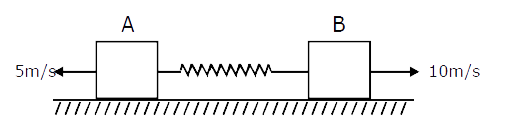
View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionA particle moves along x-axis according to relation x=1+2sinωt. The amplitude of S.H.M. is
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .
.
View Solution

