Intensity due to line source S1 at a distance of r is I0 and intensity due to other line source S2 at a distance of r is 4I0 and frequency of both source are equal. If interference occurs at a point P as shown in the figure and wavelength of both sources is r, find the resultant intensity (in wa/m2) at P. (where I0=2watt/m2)

8
4
2
1
In case of line source I∝1/r
Path difference Δx=4r−r=3r=3λ
So constructive interference occurs at P.
IP=Imax=(√I1+√I2)2=4I0
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
Knowledge Check
S1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
A1Wm−2B2Wm−2C3Wm−2D4Wm−2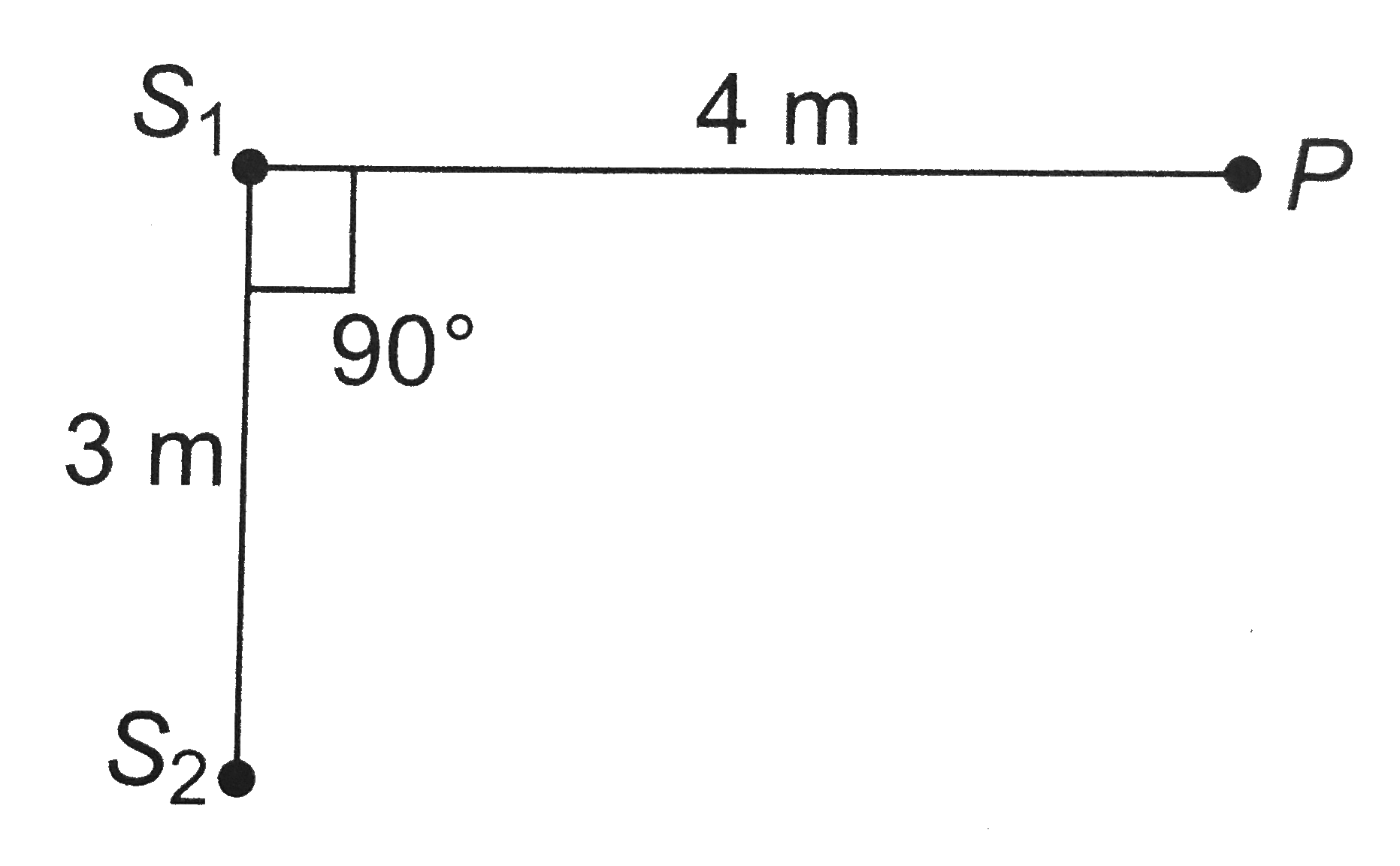
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P isAI0B9I0C3I0D8I0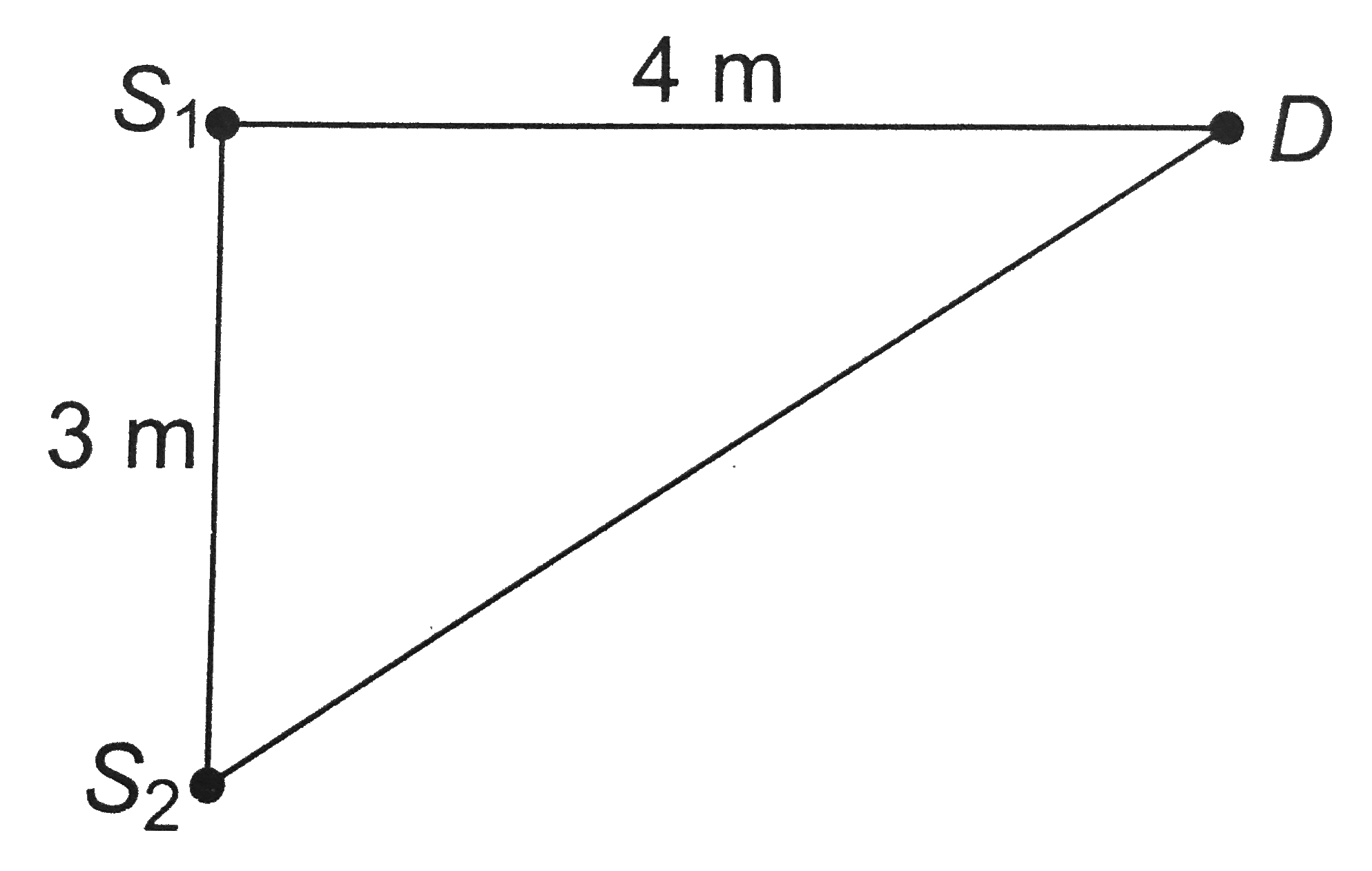
In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:A4I0BI0C2I0Dzero
Two coherent sources each emitting light of intensity I0 Interfere, in a medium at a point, where phase different between them is 2π3. Then, the resultant intensity at that point would be.
View SolutionIntensity of a point source of sound is 0.2Wm2 at a place. If the distance of source and power are doubled,the intensity at that place becomes to
View SolutionA point source of light 'S' at a distance d from the screen A produces light intensity I0 at the centre of the screen. If a completely reflecting mirror M is placed at a distance d behind the source as shown in the figure, find the intensity at the centre of the screen

View SolutionA point source of light 'S' at a distance d from the screen A produces light intensity I0 at the centre of the screen. If a completely reflecting mirror M is placed at a distance d behind the source as shown in the figure, find the intensity at the centre of the screen

View SolutionThe frequencies of sources A and B as shown in figure are same. The nature of interference at points P, Q and R will be if AB=λ2 and the two sources are in same phase.
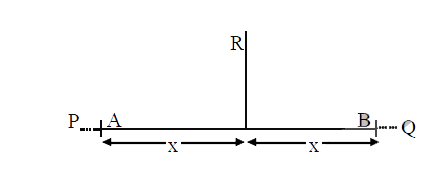
View Solution

