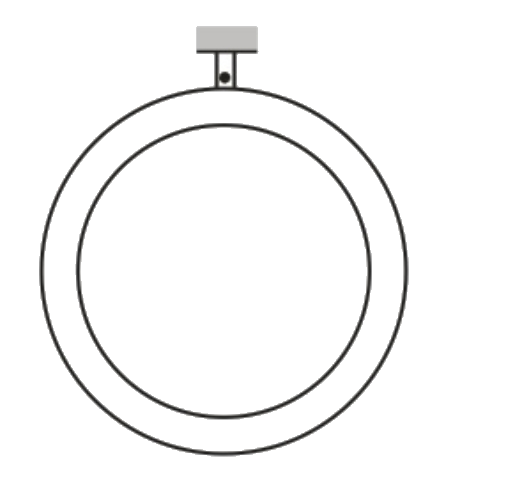
A ring of radius r is suspended from a point on its circumference. Det

A uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A $2 π \sqrt{\frac{2 R}{g}}$
B $π \sqrt{\frac{2 R}{g}}$
C $\frac{π}{2} \sqrt{\frac{R}{g}}$
D $π \sqrt{\frac{R}{2 g}}$
A uniform hoop of mass M and radius R hangs in a vertical plane supported by a knife edge at one point on the inside circumference. Calculate the natural frequency of small oscillation
A $\frac{1}{2 π} \sqrt{\frac{g}{R}}$
B $\frac{1}{2 π} \sqrt{\frac{3 g}{2 R}}$
C $\frac{1}{2 π} \sqrt{\frac{g}{2 R}}$
D $\frac{1}{2 π} \sqrt{\frac{g}{3 R}}$
A ring of radius R is suspended from its circumference and is made to oscillate about a horizontal axis in a vertical plane. The length equivalent to a simple pendulum will be :
A $2 R$
BR
C $\frac{3 R}{2}$
D(R ) /(2)

A ring of radius $r$ is suspended from a point on its circumference. Determine its angular frequency of small oscillations.