A body of mass 200g is in equibrium at x=0 under the influence of a force F(x)=(−100x+10x2)N.
(a) If the body is displacement a small distance from equilibrium, what is the period of its oscillations ?
(b) If the amplitude is 4.0cm, by how much do we eror in assuming that F(x)=−kx at the end points of the motion.
The correct Answer is:A, B, D
(a) For small displacement x, the term x2 can be neglected.
∴F=−100x
Comparing with F=−kx we have,
k=100N/m
T=2π√mk
=2π√0.2100=0.28s
(b) |ΔF|=10x2=10(0.04)2=0.016N
|F|=100x=100(0.04)=4N
∴% error =|ΔF||F|×100=0.4% .
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
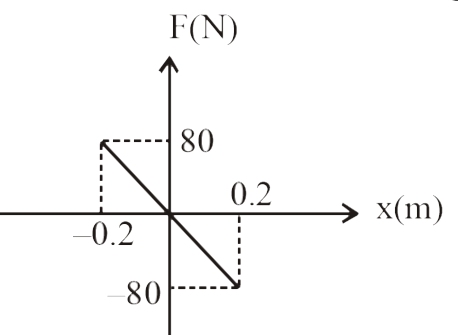
View SolutionA particle moves along x-axis from x=0 to x=2 m under the influence of a force F (in N) given by F=3x2+2x−5. Calculate the work done
View Solution
Knowledge Check
A body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
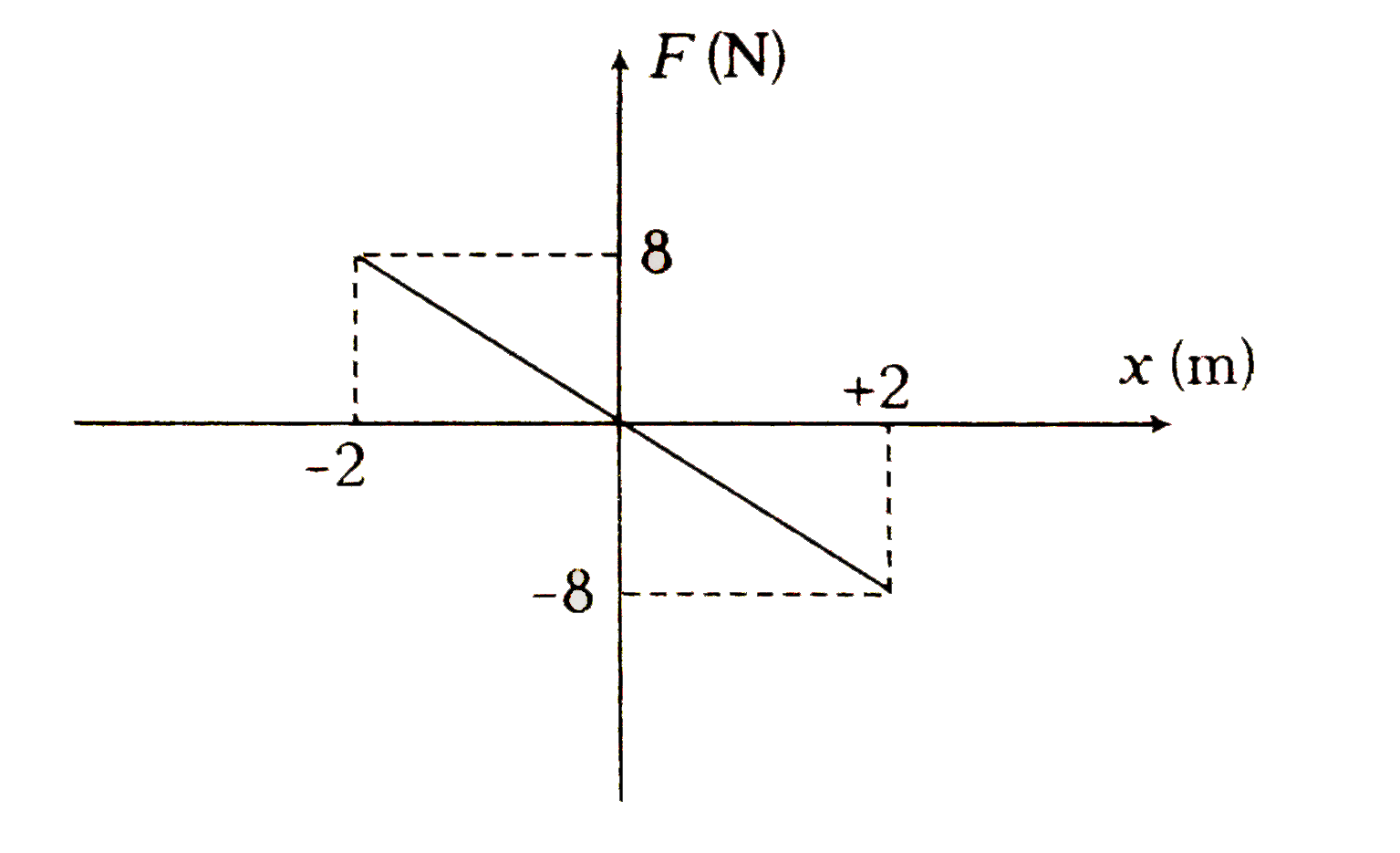 A1.05 sB0.52 sC0.25 sD0.31 s
A1.05 sB0.52 sC0.25 sD0.31 sA particle moves along the X-axis x=0 to x=5 m under the influence of a force given by F=10−2x+3x2. Work done in the process is
A70 unitsB270 unitsC35 unitsD150 unitsA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
A+4JB−4JC+8JD−8J
A particle moves under the force F(x)=(x2−6x)N, where x is in metres. For small displacements from the origin what is the force constant in the simple harmonic motion approximation ?
View SolutionA particle moves along the X-axis from x=0→x=5m under the influence of a force given by F=(7−2x+3x2). Find the work done in the process.
View SolutionA particle moves under the effect of a force F=kx2 from x=0 to x=4, the work done by force is ?
View SolutionA particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by F=7−2x+3x2. Find the work done in the process.
View SolutionA particle of mass m oscillates with a potential energy U=U0+αx2, where U0 and α are constants and x is the displacement of particle from equilibrium position. The time period of oscillation is
View Solution
