The wheel of radius R rolls without slipping on horizontal rough surface, and its centre O has an horizontal acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. For a given values of a0, R and r, determine the angle θ for which point P has no acceleration in this position.
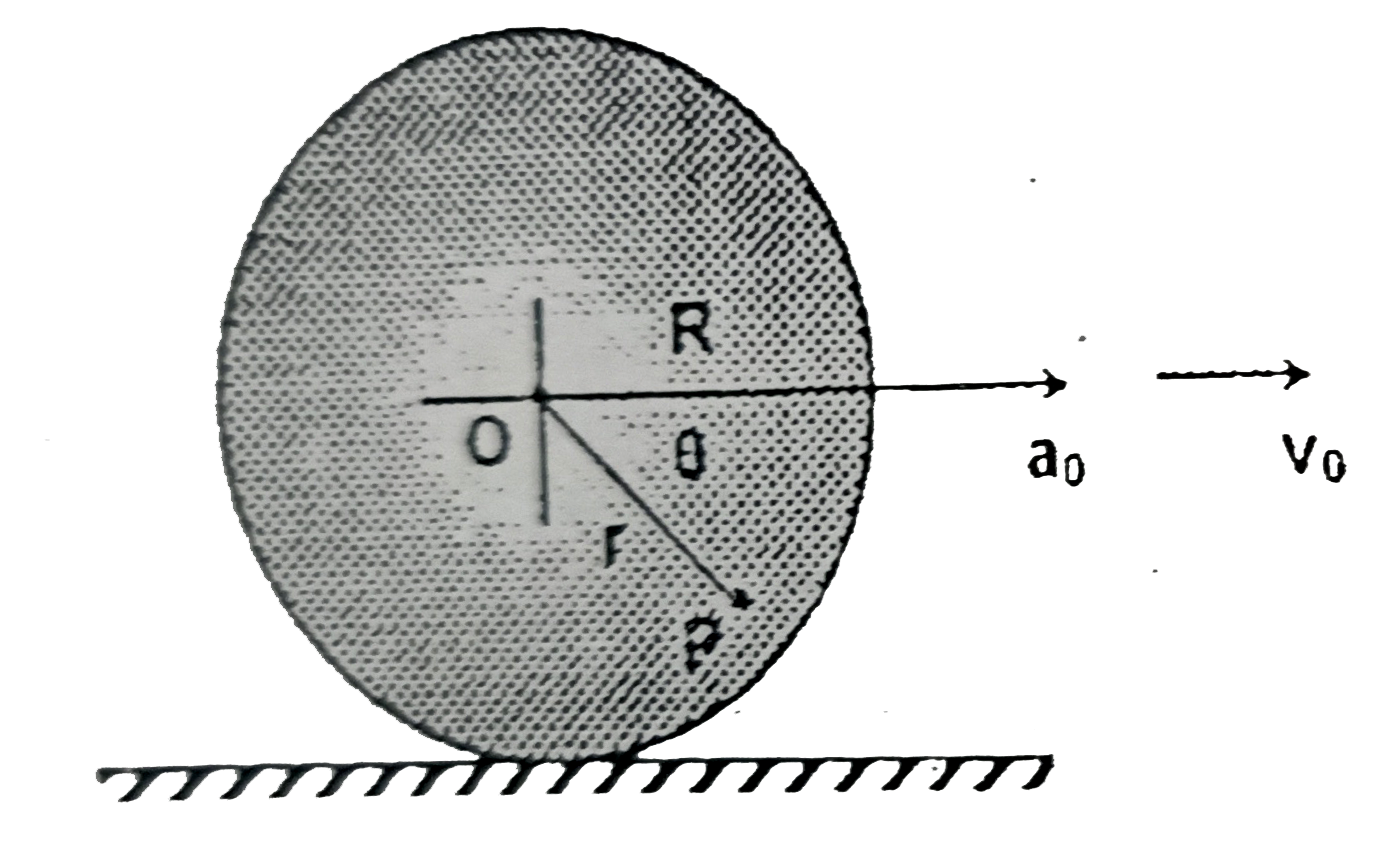
The acceleration of the point P is that due to the axis (a0) and the to rotation about the axis.
a0cosθ=ω2r
a0sinθ=αr
a0=αR

Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Objective problems
Explore 215 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
The wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. Find the angle θ for which point P can have zero acceleration in this position .

View SolutionA disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.

Speed of point P having coordinates (x,y) is
View Solution
Knowledge Check
The wheel of radius R rolls with out slipping on horizontal rough surface, and its centre O has an horizontal acceleration in a0 forward direction. A point P on the wheel is a distancer r from O and angular position θ from horizontal. For the given values of a0 R and r, determine the angle θ for which point P has no acceleration in this position.
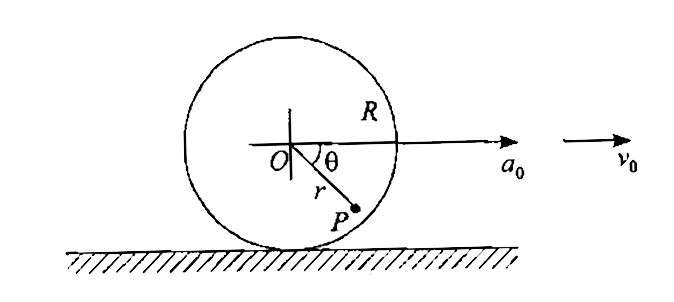 Acos1.rRBtan1.rRCsin1.rRDcos1.r2R
Acos1.rRBtan1.rRCsin1.rRDcos1.r2RThe wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. Find the angle θ for which point P can have zero acceleration in this position .
 Acos−1(r)RBtan−1(r)RCsin−1(r)RDcos−1(r)2R
Acos−1(r)RBtan−1(r)RCsin−1(r)RDcos−1(r)2RA wheel of radius R rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
A2πRB8RC2RDπR
A wheel of radius R rolls without slipping on the horizontal surface with speed v0. When the contact point is P on the road, a small patch of mud separates from the wheel at its highest point strikes the road at point Q. Find distance PQ.
View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
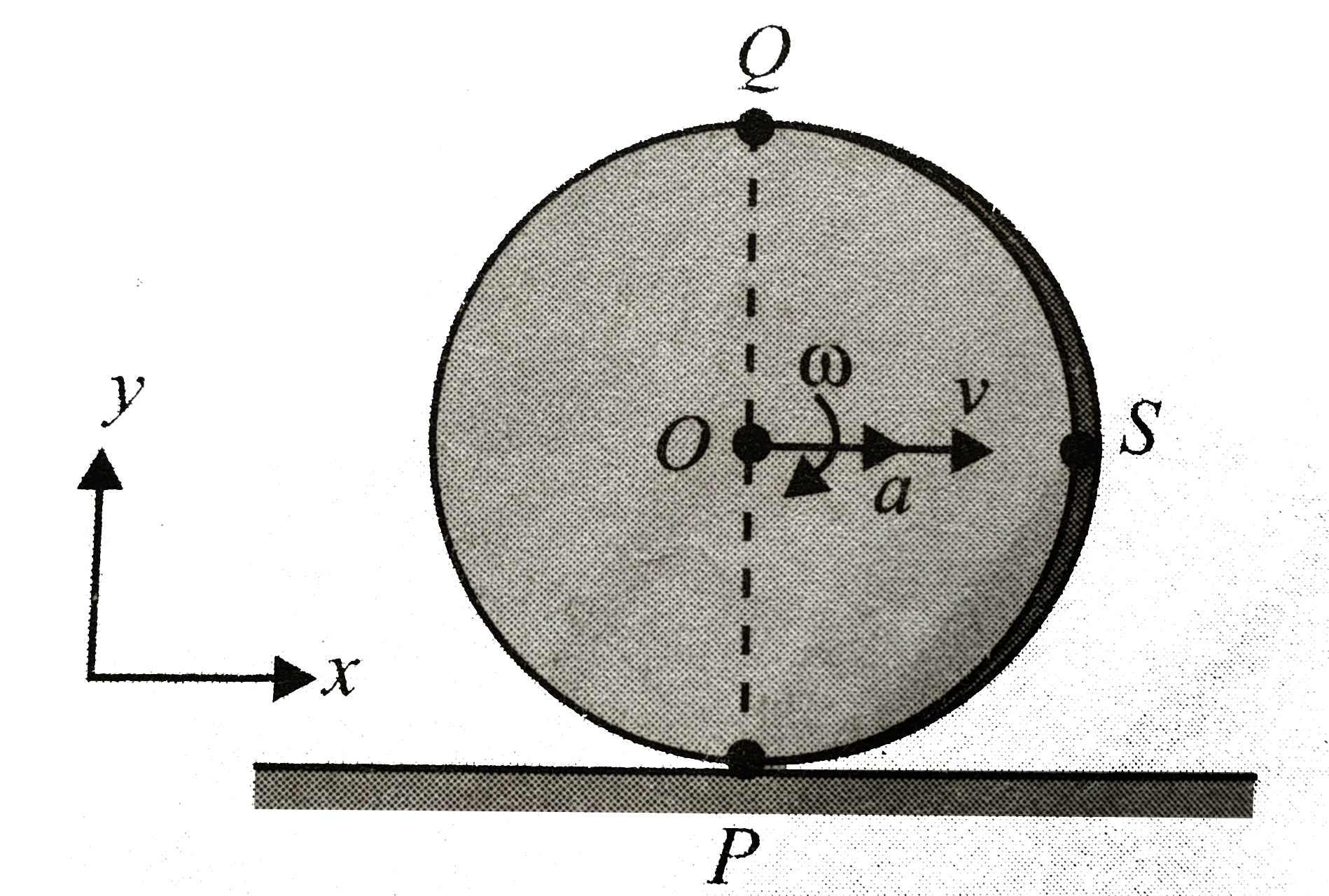
View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
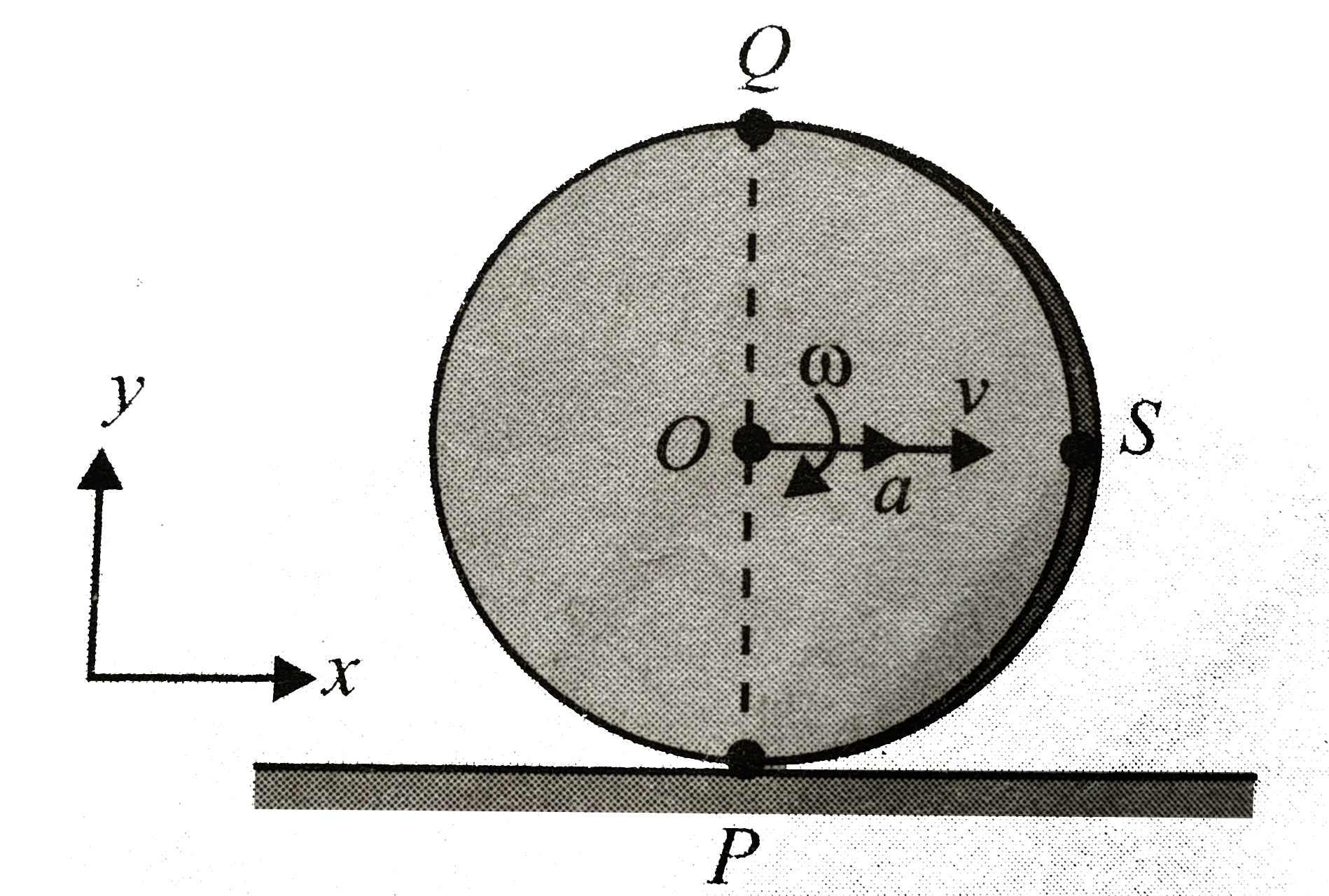
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.

Speed of point P having coordinates (x,y) is
View Solution

