Consider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
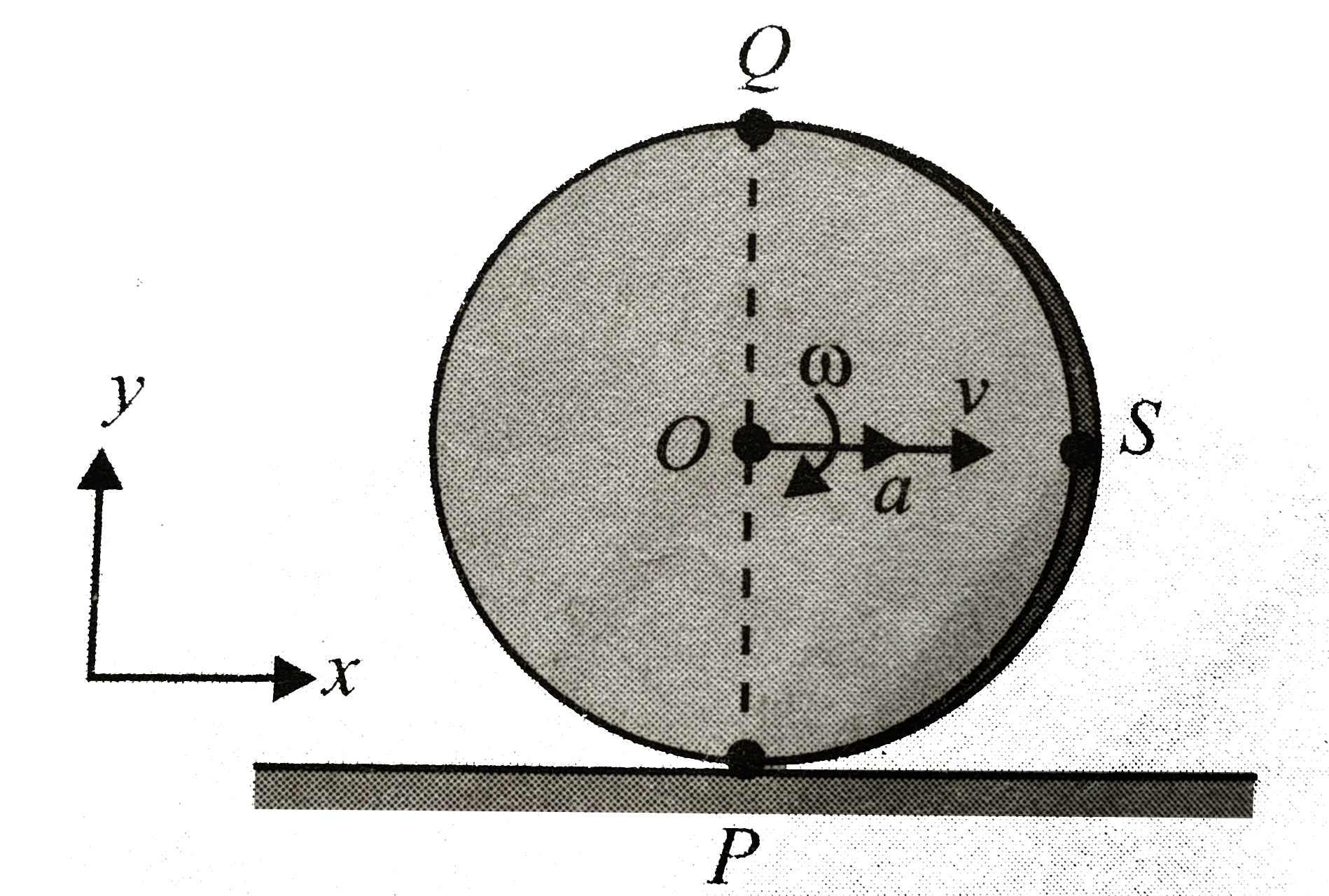
As body is rolling, we can write the following: Acceleration of cenntre of mass a=αR
Velocity of centre of mass v=ωR

From fig d. we get the following
Resultant acceleration of point O,a0=aˆi
Acceleration of p,aP=aˆi−aˆi+ω2Rˆj=ω2Rˆj
Acceleration of Q,aQ=aˆi+aˆi−ω2Rˆj=2aˆi−ω2Rˆj
Acceleration of S,as=aˆi−ω2Rˆj=(a−ω2R)ˆi−aˆj
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
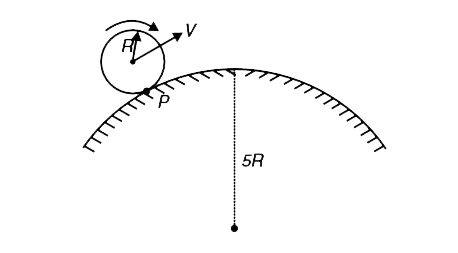
A convex surface has a uniform radius of curvature equal to 5R. A wheel of radius R is rolling without sliding on it with a constant speed v. Find the acceleration of the point (P) of the wheel which is in contact with the convex surface.
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View Solution
Knowledge Check
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
A75gsinθB27gsinθC37gsinθD57gsinθA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
A0≤v≤2uBv=u, if CP is horizontalCv=u, if CP makes an angle of 30∘ with the horizontal and P is below the horizontal level of C.Dv=√2u, if CP is horizontal.A solid sphere rolls down without slipping from rest on a 30∘ incline. Its linear acceleration is
A5g/7B5g/14C2g/3Dg/3
A constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?
View SolutionA ball of radius R=10.0cm rolls without slipping down an inclined plane so that its centre moves with constant acceleration
w=2.50cm/s2, t=2.00s after the beginning of motion its position corresponds to that shown in figure. Find:
(a) the velocities of the points A, B, and O,
(b) the accelerations of these points.

View Solution
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at
View SolutionA circular disc rolls on a horizontal floor without slipping and the centre of the disc moves with a unifonn velocity v. Which of the following values the velocity at a point on the rim of the disc can have?
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View Solution

