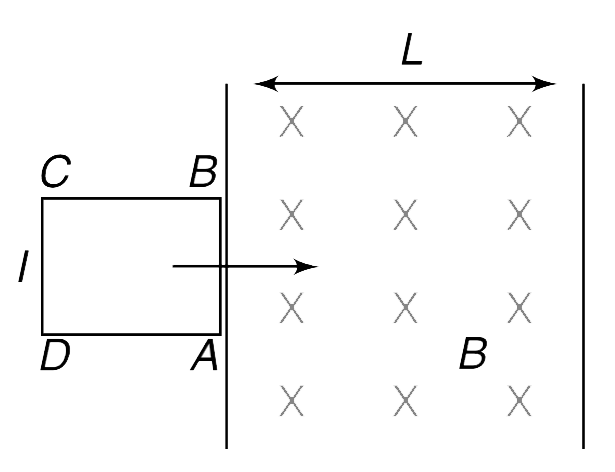
A region of width L contains a uniform magnetic field B directed into the plane of the figure. A square conducing loop of side length l(<L) is kept with its side AB at the boundary of the field region (see Figure). The loop is pushed into the field region with a speed such that it just manages to exit the field region. Calculate the time needed for the entire loop to enter the field region after it is pushed. Mass and resistance of the loop is M and R respectively.
The correct Answer is:MRln2B2l2
Step by step video, text & image solution for A region of width L contains a uniform magnetic field B directed into the plane of the figure. A square conducing loop of side length l ( lt L) is kept with its side AB at the boundary of the field region (see Figure). The loop is pushed into the field region with a speed such that it just manages to exit the field region. Calculate the time needed for the entire loop to enter the field region after it is pushed. Mass and resistance of the loop is M and R respectively. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Show the direction of the current when the loop is entering into the region II.
View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Plot a graph between the induced emf and the time of rotation for two periods of rotation.
View Solution
Knowledge Check
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to LThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπLThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπL
A space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Obtain an expression for the magnitude of the induced current in the loop.
View SolutionA square loop of side length L carries a current which produces a magnetic field B0 at the centre (O) of the loop. Now the square loop is folded into two parts with one half being perpendicular to the other (see fig). Calculate the magnitude of magnetic field at the centre O.

View SolutionThe magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is
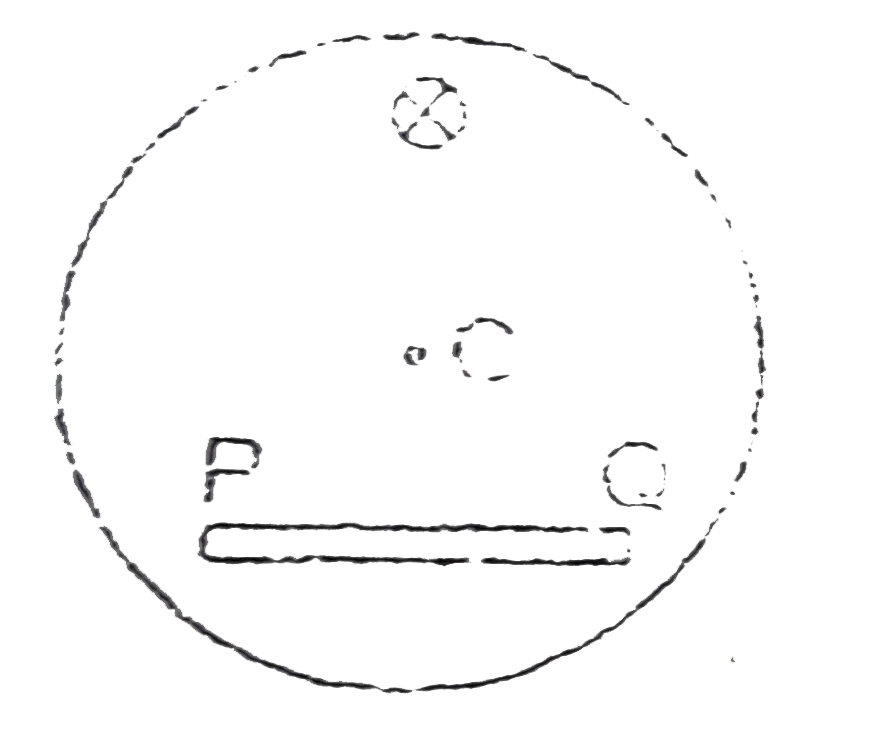
View SolutionIn a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
View SolutionA square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
View Solution

