A square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
BRlv
B2l2v2R
Bl2v2R
BvlR
The correct Answer is:B
To solve the problem, we need to determine the power required to pull a square loop of side L and resistance R out of a uniform magnetic field B at a constant velocity v. Here’s a step-by-step solution:
Step 1: Determine the induced EMF
When the loop is pulled out of the magnetic field, an electromotive force (EMF) is induced in the loop due to the change in magnetic flux. The induced EMF (E) can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
Where Φ is the magnetic flux. The magnetic flux through the loop is given by:
Φ=B⋅A=B⋅(L2)
As the loop is pulled out of the magnetic field, the area A that is in the magnetic field changes. The rate of change of flux can be expressed as:
dΦdt=B⋅L⋅v
Thus, the induced EMF is:
E=B⋅L⋅v
Step 2: Calculate the induced current
Using Ohm's law, the induced current I in the loop can be calculated as:
I=ER=B⋅L⋅vR
Step 3: Calculate the force on the loop
The force F acting on the loop due to the magnetic field can be calculated using the formula:
F=I⋅L⋅B
Substituting the expression for I:
F=(B⋅L⋅vR)⋅L⋅B=B2⋅L2⋅vR
Step 4: Calculate the power required
The power P required to pull the loop out of the magnetic field at constant velocity v is given by:
P=F⋅v
Substituting the expression for F:
P=(B2⋅L2⋅vR)⋅v=B2⋅L2⋅v2R
Final Answer
Thus, the power needed to pull the loop out of the magnetic field is:
P=B2⋅L2⋅v2R
When the loop is pulled out of the magnetic field, an electromotive force (EMF) is induced in the loop due to the change in magnetic flux. The induced EMF (E) can be calculated using Faraday's law of electromagnetic induction:
Using Ohm's law, the induced current I in the loop can be calculated as:
The force F acting on the loop due to the magnetic field can be calculated using the formula:
The power P required to pull the loop out of the magnetic field at constant velocity v is given by:
Thus, the power needed to pull the loop out of the magnetic field is:
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A rectangular loop of wire is placed in a uniform magnetic field B acting normally to the plane of the loop. If a man attempt to pull it out ofthefield with velocityv as shown in figure-5.338, calculate the power required for this purpose.
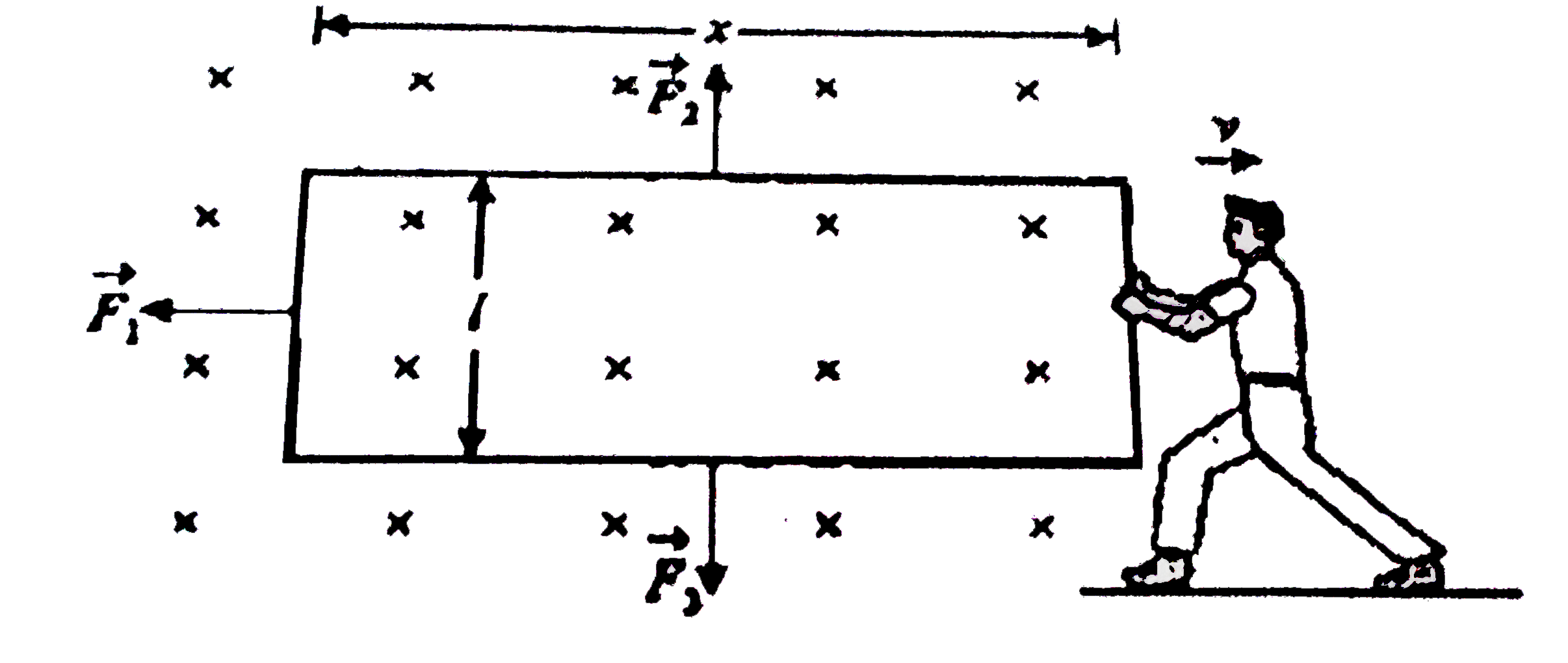
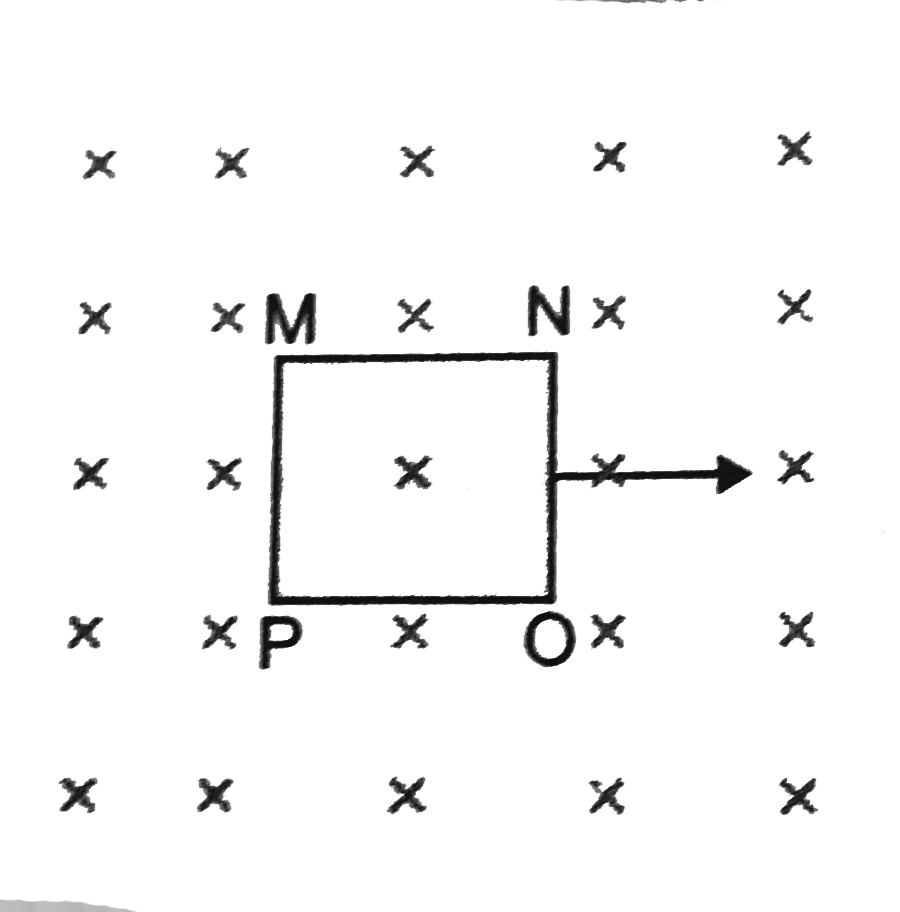
View SolutionA square loop MNOP of side 20 cm is placed horizontally in a uniform magnetic field acting vertically downwards as shown in Fig. The loop is pulled with a constant velocity of 20cm/s till it goes out of the field.
View Solution
Knowledge Check
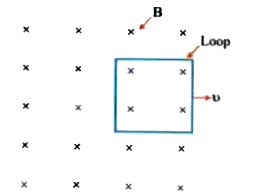
A square loop is placed in a uniform magnetic field →B as shown in fig. The power needed to pull it out of the field with a velocity v is proportional to
 Av1/2BvCv2Dv3/2
Av1/2BvCv2Dv3/2A triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
AZeroBIBlC√32II2B2D√34IBl2A triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
AZeroBIB1C√32Il2B2D√34IBl2
A square loop of a conducting material of side l and resistance r is dragged through a uniform magnetic field B with uniform velocity v keeping the plane of the loop perpendicular to the direction of the field. What is the current flowing through the loop?
View SolutionA triangle loop of side l carries a steady current. It is placed in a magnetic field B such that normal of the place of loop is in the direction of B, the torque on the loop is ________
View SolutionA triangular loop of side 1 carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is parallel to the plane of the loop. The magnetic torque acting on the loop is-
View SolutionA rectangular loop sides 10 cm and 3 cm moving out of a region of uniform magnetic field of 0.5T directed normal to the loop. If we want to move loop with a constant velocity 1cm/sec. Then required mechanical force is (Resistance of loop =1mΩ):-
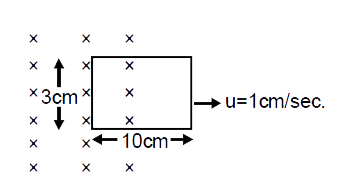
View Solution
