A time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)
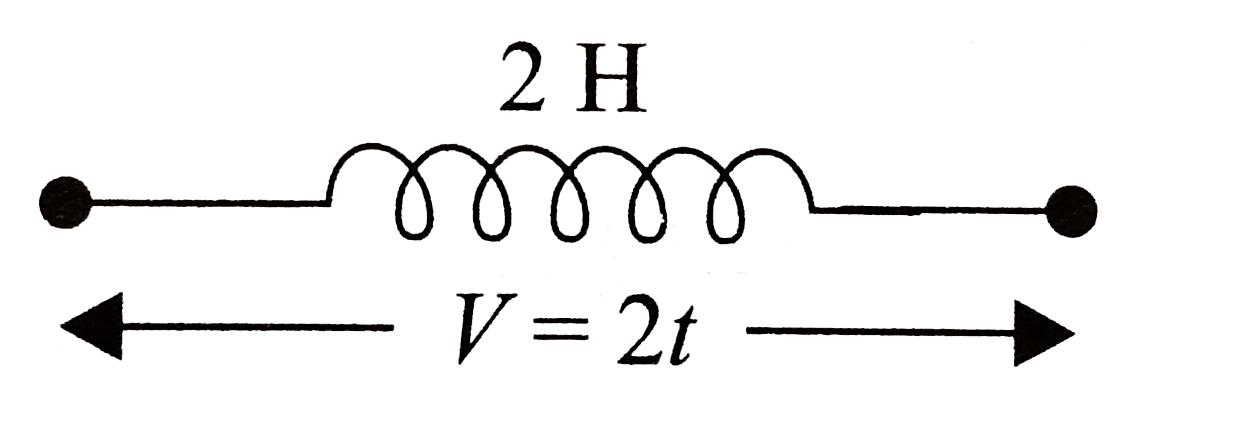
current versus time graph is a parabola
energy stored in magnetic field at t = 2 s is 4 J
potential energy at time t = 1 s in magnetic field is increasing at a rate of 1Js−1
energy stored in magnetic field is zero all the time.
The correct Answer is:A, B, C
(a, b, c) We have, V = 2t
∴ V=L.didt=2tor2.didt=2tordidt=t
or (di)=t(dt)
On integrating, we get i=t22
i.e., i-t graph is a parabola.
At t = 2 s, i= 2 A
∴ Potential energy, U=12Li2=12×2×4=4J
dUdt=Li(didt)=(2)(r22)(t)=t3
At t = 1
Potential energy, dUdt=1Js−1
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrance special format questions
Explore 17 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Match the columns
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Check point
Explore 60 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
Knowledge Check
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent l(t) leads voltage V(t) by 180∘BCurrent l(t) lags voltage V(t) by 90∘COver a full cycle the capacitor C does not consume any energy from the voltage sourceDCurrent l(t) is in phase with voltage V(t)A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent I(t), lags voltage V(t) by 90∘BOver a full cycle the capacitor C does not consume any energy from the voltage source.CCurrent I(t) is in phase with voltage V(t)DCurrent I(t) leads voltage V(t) by 180∘A sinusoidal voltage V(t) = 100 sin (500t) is applied across a pure inductance of L = 0.02 H. the current through the coil is
A10 cos (500t).B−10 cos (500t).C10 sin (500t)D−10 sin (500t)
An voltage, E=E0sinωt is applied acorss an inductor L. Obtain an expression for the current.
View SolutionAlternating voltage V = 400 sin (500πt) is applied across a resistance of 0.2kΩ. The r.m.s. value of current will be equal to
View SolutionAlternating voltage V = 400 sin (500πt) is applied across a resistance of 0.2kΩ. The r.m.s. value of current will be equal to
View SolutionA sinusoidal voltage V(t)=100sin(500t) is applied across a pure inductance of L=0.02H. The current through the coil is :
View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t = 0, current is zero.
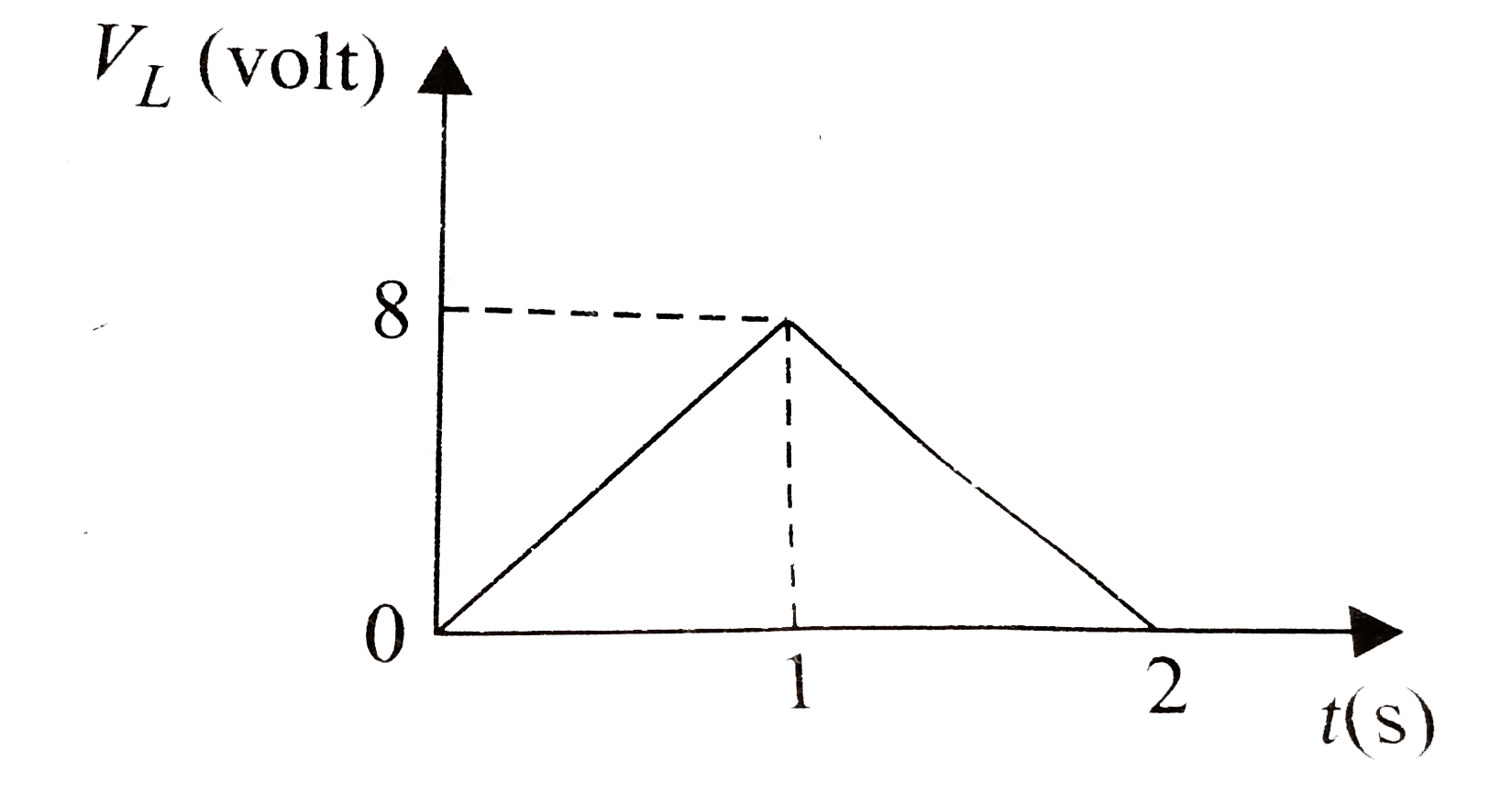
Current at t = 1 s is
View Solution

