A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is parallel to the plane of the loop. The magnetic torque acting on the loop is-
irB
2πriB
zero
πr2iB
The correct Answer is:D
To solve the problem of finding the magnetic torque acting on a conducting circular loop in a uniform magnetic field, we can follow these steps:
1. Identify the Given Information:
- A conducting circular loop of radius r carries a constant current i.
- The loop is placed in a uniform magnetic field B that is parallel to the plane of the loop.
2. Understand the Concept of Torque:
- The magnetic torque τ acting on a current-carrying loop in a magnetic field is given by the formula:
τ=m×B
- Where m is the magnetic moment of the loop.
3. Calculate the Magnetic Moment:
- The magnetic moment m for a loop is given by:
m=i⋅A
- Here, A is the area of the loop. For a circular loop, the area A is:
A=πr2
- Therefore, the magnetic moment can be expressed as:
m=i⋅πr2
4. Determine the Angle Between m and B:
- Since the magnetic field B is parallel to the plane of the loop, the angle θ between the magnetic moment m (which is perpendicular to the plane of the loop) and the magnetic field B is 90∘.
5. Calculate the Torque:
- The torque can now be calculated using the formula:
τ=m⋅B⋅sin(θ)
- Since θ=90∘, sin(90∘)=1:
τ=m⋅B
- Substituting the expression for m:
τ=(i⋅πr2)⋅B
- Thus, the final expression for the magnetic torque is:
τ=πr2iB
Final Answer:
The magnetic torque acting on the loop is:
τ=πr2iB
- A conducting circular loop of radius r carries a constant current i.
- The loop is placed in a uniform magnetic field B that is parallel to the plane of the loop.
- The magnetic torque τ acting on a current-carrying loop in a magnetic field is given by the formula:
τ=m×B
- Where m is the magnetic moment of the loop.
- The magnetic moment m for a loop is given by:
m=i⋅A
- Here, A is the area of the loop. For a circular loop, the area A is:
A=πr2
- Therefore, the magnetic moment can be expressed as:
m=i⋅πr2
- Since the magnetic field B is parallel to the plane of the loop, the angle θ between the magnetic moment m (which is perpendicular to the plane of the loop) and the magnetic field B is 90∘.
- The torque can now be calculated using the formula:
τ=m⋅B⋅sin(θ)
- Since θ=90∘, sin(90∘)=1:
τ=m⋅B
- Substituting the expression for m:
τ=(i⋅πr2)⋅B
- Thus, the final expression for the magnetic torque is:
τ=πr2iB
The magnetic torque acting on the loop is:
τ=πr2iB
Similar Questions
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
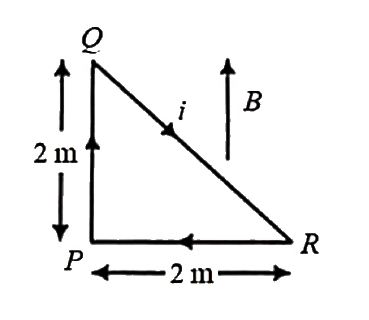
View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
AI r BB2πrIBCzeroDπrIBA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
AzeroBir BC2π ir BDπirBA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field→B such that vecB is perpendicular to the plane of the loop. What is the torque acting on the loop?
AzeroBir→BC3πri→BDnone of these
A conducting circular loop of radius r carries a constant i. It is placed in a uniform magnetic field B such that B is perpendiclar to the plane of thre loop is .What is the magnetic force acting on the loop?
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA rectangular loop of sides 20cm and 10cm carries a current of 5.0A. A uniform magnetic field of magnitude 2T exists parallel to the longer side of the loop. The torque acting on the loop is
View Solution

