A space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Show the direction of the current when the loop is entering into the region II.
To solve the problem, we need to determine the direction of the induced current when the semicircular conducting loop enters the region with a uniform magnetic field directed into the paper. We will apply Lenz's law, which states that the direction of induced current will be such that it opposes the change in magnetic flux through the loop.
1. Identify the Regions:
- Region I is field-free (no magnetic field).
- Region II has a uniform magnetic field B directed into the paper.
2. Understand the Motion of the Loop:
- The semicircular loop ACD is rotating with a constant angular velocity ω about an axis through point O, which is perpendicular to the plane of the paper.
- As the loop rotates, it will eventually enter region II where the magnetic field is present.
3. Determine the Change in Magnetic Flux:
- When the loop enters region II, the area of the loop that is exposed to the magnetic field increases, leading to an increase in magnetic flux through the loop.
- The magnetic flux Φ through the loop can be expressed as:
Φ=B⋅A
- As the loop enters the magnetic field, the area A exposed to the field increases, resulting in an increase in flux.
4. Apply Lenz's Law:
- According to Lenz's law, the induced current will flow in a direction that opposes the change in magnetic flux.
- Since the magnetic field is directed into the paper and the flux is increasing as the loop enters region II, the induced current must create a magnetic field that opposes this increase.
5. Determine the Direction of the Induced Current:
- To oppose the increase in the magnetic flux (which is directed into the paper), the induced current must generate a magnetic field that is directed out of the paper.
- Using the right-hand rule, if the current flows in an anticlockwise direction around the loop, the magnetic field produced by this current will be directed out of the paper.
- Therefore, when the loop is entering region II, the direction of the induced current will be anticlockwise.
Conclusion:
The direction of the induced current when the loop is entering into region II is anticlockwise.
---
- Region I is field-free (no magnetic field).
- Region II has a uniform magnetic field B directed into the paper.
- The semicircular loop ACD is rotating with a constant angular velocity ω about an axis through point O, which is perpendicular to the plane of the paper.
- As the loop rotates, it will eventually enter region II where the magnetic field is present.
- When the loop enters region II, the area of the loop that is exposed to the magnetic field increases, leading to an increase in magnetic flux through the loop.
- The magnetic flux Φ through the loop can be expressed as:
Φ=B⋅A
- As the loop enters the magnetic field, the area A exposed to the field increases, resulting in an increase in flux.
- According to Lenz's law, the induced current will flow in a direction that opposes the change in magnetic flux.
- Since the magnetic field is directed into the paper and the flux is increasing as the loop enters region II, the induced current must create a magnetic field that opposes this increase.
- To oppose the increase in the magnetic flux (which is directed into the paper), the induced current must generate a magnetic field that is directed out of the paper.
- Using the right-hand rule, if the current flows in an anticlockwise direction around the loop, the magnetic field produced by this current will be directed out of the paper.
- Therefore, when the loop is entering region II, the direction of the induced current will be anticlockwise.
The direction of the induced current when the loop is entering into region II is anticlockwise.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:MOTIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-1
Explore 25 Videos
- ELECTROMAGNETIC INDUCTIONBook:MOTIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-2 (LEVEL-I)
Explore 16 Videos
- ELECTRO MAGNETIC WAVES Book:MOTIONChapter:ELECTRO MAGNETIC WAVES Exercise:EXERCISE - 3 (SECTION - B)
Explore 8 Videos
- ELECTROMAGNETISMBook:MOTIONChapter:ELECTROMAGNETISMExercise:Exercise
Explore 136 Videos
Similar Questions
A space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Obtain an expression for the magnitude of the induced current in the loop.
View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Plot a graph between the induced emf and the time of rotation for two periods of rotation.
View Solution
Knowledge Check
There is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
Acurrent is induced in the loop in the anticlockwise directionBcurrent is induced in the loop in the clockwise directionCAltrenating current is induced in the loopDno current is induced in the loopA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
 AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξs
AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξsIn figure, there is conducting ring having resistance R placed in the plane of paper in a uniform magnetic field B0. If the rings is rotating in the plane of paper about an axis passing through point O and perpendicular to the plane of paper with constant angular speed ω in clockwise direction, then
 Apoint O will be at higher potential than ABthe potential of point B and C will be differentCthe current in the ring will be zeroDthe current in the ring will be 2B0ωr2/R
Apoint O will be at higher potential than ABthe potential of point B and C will be differentCthe current in the ring will be zeroDthe current in the ring will be 2B0ωr2/R
Space is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
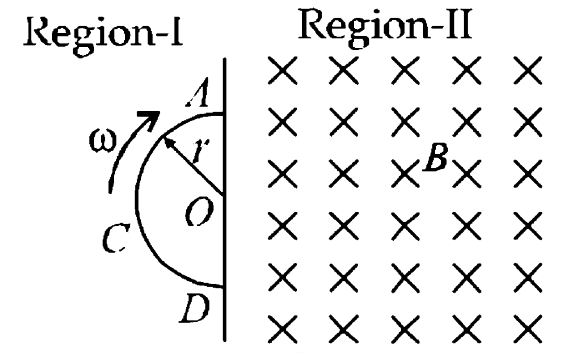
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.

View SolutionThere exists a uniform magnetic field ¯¯¯B=B0t¯k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View SolutionA uniform magnetic field B=B0tˆi in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
View SolutionPredict the direction of the induced current in the rectangular loop abcd as it is moved into the region of a uniform magnetic filed →B directed normal to the plane of the loop.

View Solution

