A contaienr havng an ideal liquid of density ρ is moving with a constant acceleration of ˆa=axˆi+azˆk where x direction is horizontal and z is vertically upwards. The container is open at the top. In a reference frame attached to the contaienr with origin at bottom corner (see figure), write the pressure at a point inside the liquid at co-ordinates (x,y,z). The pressure is P0 at origin.
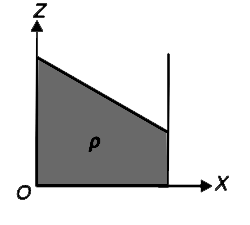
The correct Answer is:P=P0−ρax,x−ρ(g+az)z
Step by step video, text & image solution for A contaienr havng an ideal liquid of density rho is moving with a constant acceleration of hata=a_(x)hati+a_(z)hatk where x direction is horizontal and z is vertically upwards. The container is open at the top. In a reference frame attached to the contaienr with origin at bottom corner (see figure), write the pressure at a point inside the liquid at co-ordinates (x,y,z). The pressure is P_(0) at origin. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View SolutionTwo lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p_(0) is (take rho as the density of liquid)
View Solution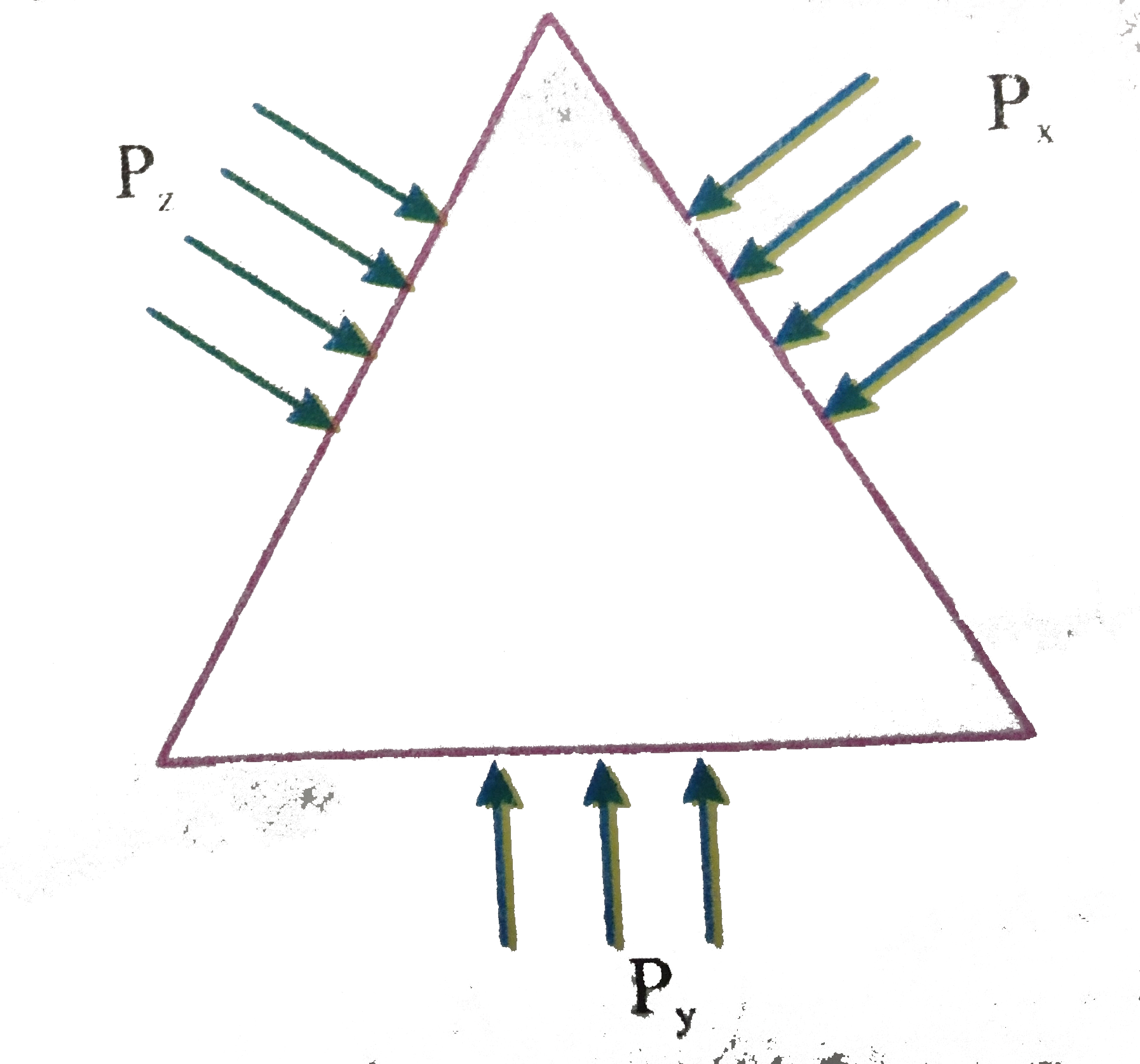
A triangular element of the liquid is shown in the fig. Px,Py and Pz represent the pressures on the element of the liquid then:
View SolutionA vertical communicating tube contains a liquid of density rho . If it moves with a horizontal acceleration a , pressure at A is equal to :
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionThe component of vector A=axˆi+ayˆj+azˆk and the directioin of ˆi−ˆj is
View Solutionयदि →A=Axˆi+Ayˆj+Azˆk तथा →B=Bxˆi+Byˆj+Bzˆk है, तो सिद्ध कीजिए कि →A×→B=−→B×→A.
View Solution(a) यदि सदिश →A=Axˆi+Ayˆj+Azˆk तथा सदिश →B=Bxˆi+Byˆj+Bzˆk के बीच का कोण θ हो, तो सिद्ध कीजिए कि
cosθ=AxBx+AyBy+AzBz√A2x+A2y+A2z√B2x+B2y+B2z
(b) सदिश (ˆi+ˆj) तथा (ˆj+ˆk) के बीच कोण कितना होगा ?
View SolutionThe component of vector A=(axˆi+ayˆkazˆk) along the direction of (i - j) is
View SolutionConsider a vessel filled with a liquid upto height H. The bottom of the vessel lies in the XY-plane passing through the origin. The density of the liquid varies with Z-axis as ρ(z)=ρ0[2−(zH)2]. If p1 and p2 are the pressures at the bottom surface and top surface of the liquid, the magnitude of (p1−p2) is
View SolutionThe component of vector vecA = a_(x) hati+ a_(y) hatj + a_(z) hatk along th direction of (hati - hatj) is
View SolutionA sealed tank containing a liquid of density rho moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
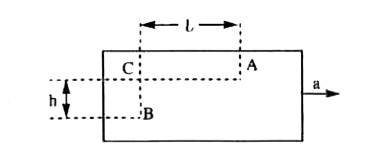
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View Solution
