Force acting on a particle in a two dimensional XY space is given as →F=3(Xˆi+Yˆj)((X92)+Y2)3/2⎞⎟ ⎟⎠. Show that the force is conservative.
Step by step video, text & image solution for Force acting on a particle in a two dimensional XY space is given as vec(F)=(3(Xhati+Yhatj))/((X^92)+Y^(2))^(3//2)). Show that the force is conservative. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Force acting on a particle varies with the distance travelled by the particle as F prop(1)/((x)^(1/3)) then power due to this force varies with as:
View SolutionThe potential energy function of a particle in a region of space is given as U=(2xy+yz) J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View Solution
Knowledge Check
The potential energy (in joules ) function of a particle in a region of space is given as:
U=(2x2+3y2+2x)
Here x,y and z are in metres. Find the maginitude of x compenent of force ( in newton) acting on the particle at point P ( 1m, 2m, 3m).A2B3C0D4Consider a force acting on a particle given as →F=yˆi+xˆj , where ( x, y ) is the instantaneous location of the particle. This type of force is :
ASurely a conservation forceBSurely a non-conservation forceCInformation insufficient to reach to a conclusionDWill be conservation only if the particle is constrained to move in the x-y plane.Assertion: If the positon vector of a particle moving in space is given by →r=2tˆi−4t2ˆj, then the particle moves along a parabolic trajector.
Reason: →r=xˆi+yˆj and →r=2tˆi−4t2j
⇒y=−x2.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are false
The position vector of a particle of mass m= 6kg is given as →r=[(3t2−6t)ˆi+(−4t3)ˆj]m. Find:
(i) The force (→F=m→a) acting on the particle.
(ii) The torque (→τ=→r×→F) with respect to the origin, acting on the particle.
(iii) The momentum (→p=m→v) of the particle.
(iv) The angular momentum (→L=→r×→p) of the particle with respect to the origin.
View SolutionForce acting on particle is given by →F=2xyzˆi+x2xˆj+x2yˆk. Report the amount of work done in joule in displacing a particle of mass 2 kg from (0, 0, 0) to (1, 2, 3), acted upon by the given force.
View SolutionA force acting on a certain particle depends of the particles position in the xy-plane. This force F is given by the expression
→F=(xyˆi+xyˆj)(1N/m2)
where x and y are expressed in metre. If →F is a conservation force ?
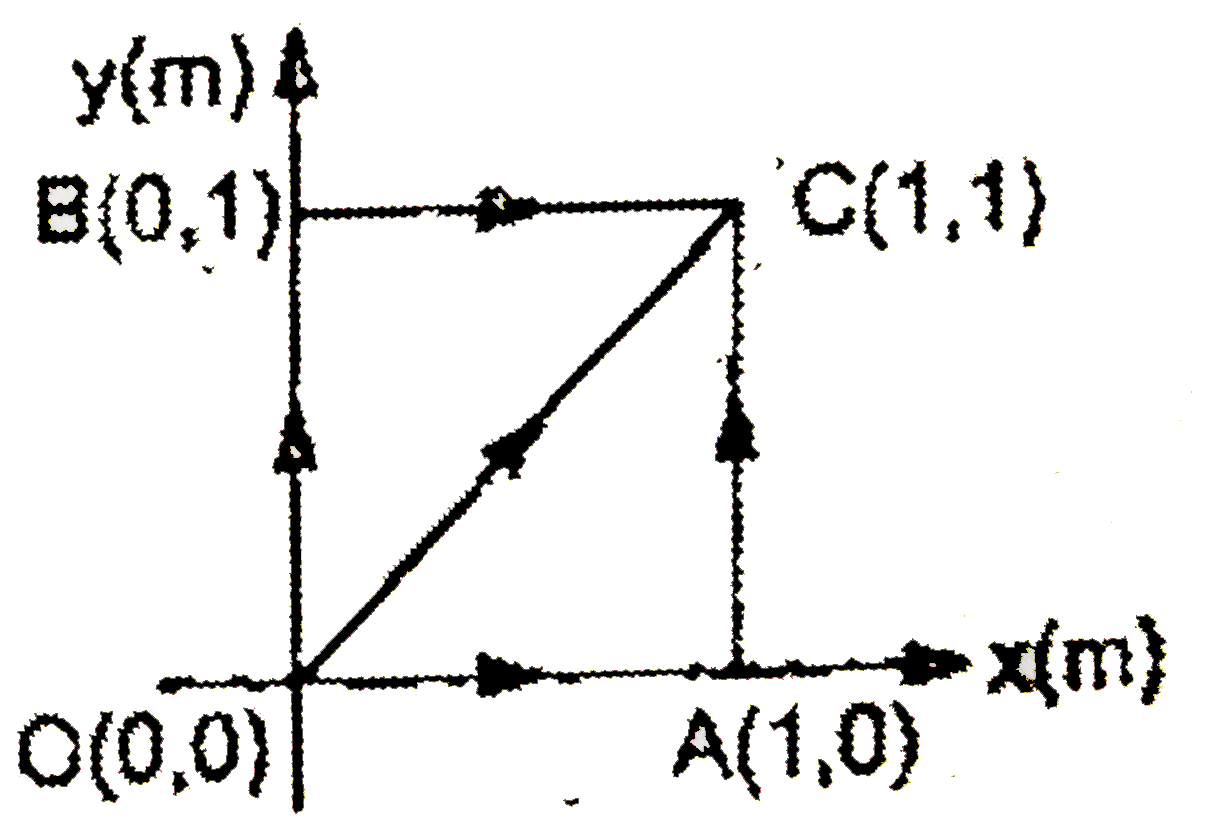
View SolutionA particle is moved along the different paths OAC,OBC&ODC as shown in the figure . Path ODC is a parabola , y=4x2. Find the work done by a forc →F=xyˆi+x2y on the particle along these paths. Is this force a conservative force ?
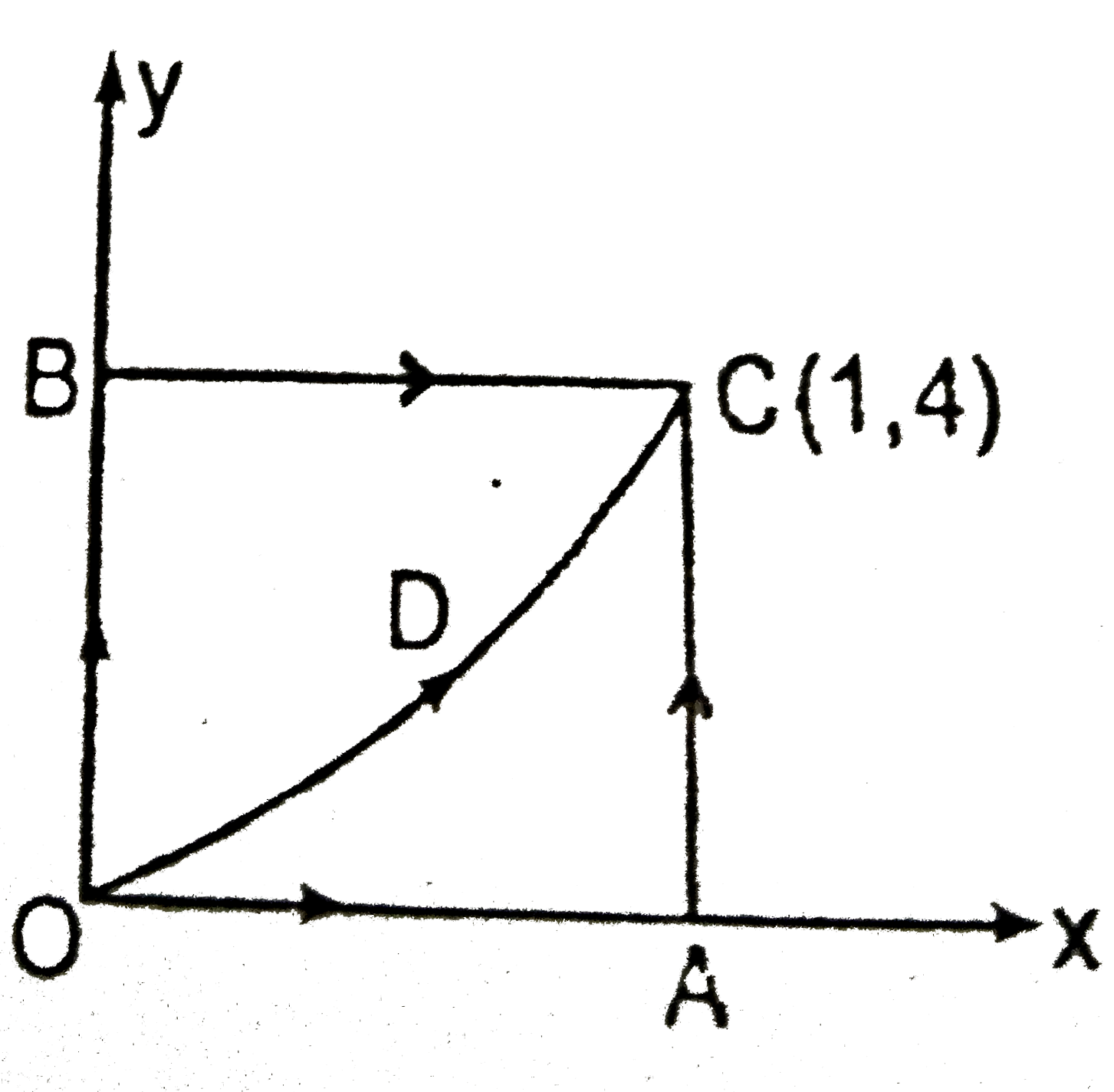
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View Solution
