A particle of mass m moves in xy plane such that its position vector, as a function of time, is given by →r=b(kt−sinkt)ˆi+b(kt+coskt)ˆj. where b and k are positive constants. (a) Find the time t0 in the interval o≤t≤πk when the resultant force acting on the particle has zero power. (b) Find the work done by the resultant force acting on the particle in the interval to≤t≤π4
The correct Answer is:(a) t0=π4K
(b) W=((1+2sqrt(2))/2) mb^(2)k(
Step by step video, text & image solution for A particle of mass m moves in xy plane such that its position vector, as a function of time, is given by vec(r) =b(kt-sinkt)hati+b(kt+cos kt) hatj. where b and k are positive constants. (a) Find the time t_0 in the interval o le t le (pi)/k when the resultant force acting on the particle has zero power. (b) Find the work done by the resultant force acting on the particle in the interval t_(o) le t le (pi)/4 by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle moves in xy plane with its position vector changing with time (t) as →r=(sint)ˆi+(cost)ˆj ( in meter)
Find the tangential acceleration of the particle as a function of time. Describe the path of the particle.
View SolutionThe position vector of a particle is given by →r=kcosωˆi+ksinωˆj=xˆi+yˆj, where k and ω are constants and t time. Find the angle between the position vector and the velocity vector. Also determine the trajectory of the particle.
View Solution
Knowledge Check
A particle moves on the xy-pane such that its position vector is given by →r=3t2ˆi−t3ˆj. The equation of trajectory of the particle is given by
A3x2+16y=0B(3x2)4/3+4y=0C(x32)3/2+y=0Dnone of theseVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
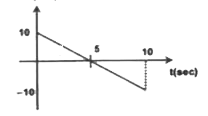 A300JB−300JCzeroD−400J
A300JB−300JCzeroD−400JThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is
 A(a) 300JB(b) −300JC(c) 400JD(d) −400J
A(a) 300JB(b) −300JC(c) 400JD(d) −400J
A particle moves in the xy plane under the influence of a force such that its linear momentum is →P(t)=A[ˆicos(kt)−ˆjsin(kt)], where A and k are constants. The angle between the force and momentum is
View SolutionA particle moves in the x-y plane under is influence of a force such that its linear momentum is →P(t)=A[ˆicos(kt)−ˆjsin(kt)], where A and k are constants Angle between the force and the momentum is:
View SolutionA particle is moving such that its position vector varies with time as →r=(1−αt)t→A, where α and →A are constant quantities. At t=0, the particle is at a position O. At some later instant 't0', the particle is again at O. Velocity of the particle at the instant t0 is:
View SolutionA particle moves in the XY-plane according to the law x=kt,y=kt(1−αt), where k and α are positive constants and t is time. The trajectory of the particle is
View SolutionA particle moves in the X-Y plane under the influence of a force such that its linear momentum is →p(t)=A[ˆicos(kt)−ˆjsin(kt)], where A and k are constants. The angle between the force and the momentum is
View Solution
