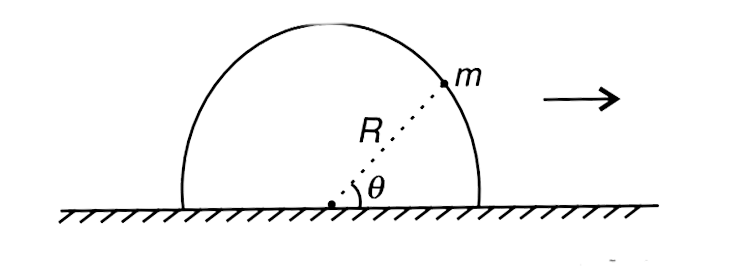
A semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
The correct Answer is:√2gR(1+cosθ0sinθ0)
Step by step video, text & image solution for A semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
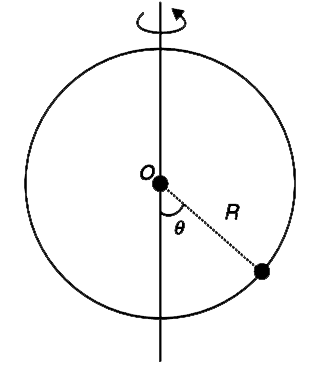
A circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
View SolutionA board is balanced on a rough horizontal semicircular log. Equilibrium is obtained with the help of addition of a weight to one of the ends of the board when the board makes an angle θwith the horizontal. Coefficient of friction between the log and the board is
View Solution
Knowledge Check
A small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 AvRB2vRCv2RD3vR
AvRB2vRCv2RD3vRA bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
A√2gRB√2gR(1−sinθ)C√2gR(1−cosθ)D2√gRA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
A√2grB√2gr(1−sinθ)C√2gr(1−cosθ)D2√gr
Find the coordination of the centre of mass of a uniform semicircular wire of radius R and mass M.
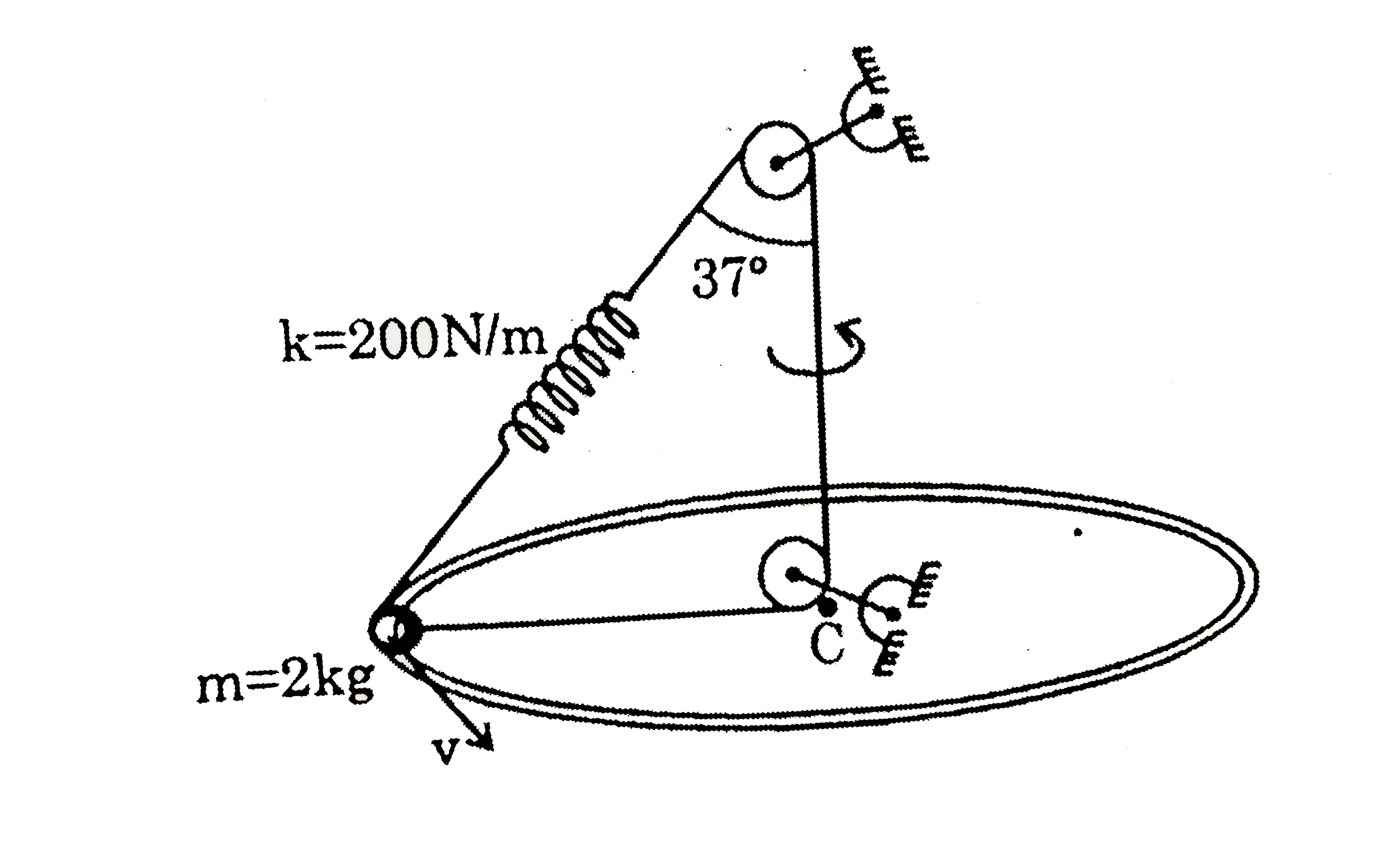
View SolutionA bead is moving on a frictionless fixed circular wire of radius 0.8 m in horizontal plane with constant speed & there is no interaction force between bead & wire & it is also connected with string & spring .
View SolutionA rigid triangular frame ABC of mass m is hanging from a rigid horizontal rod PQ. The frame is constrained to move along horizontal without friction. A bead of mass m is released from B that moves along BC. Displacement of frame when bead reaches C is
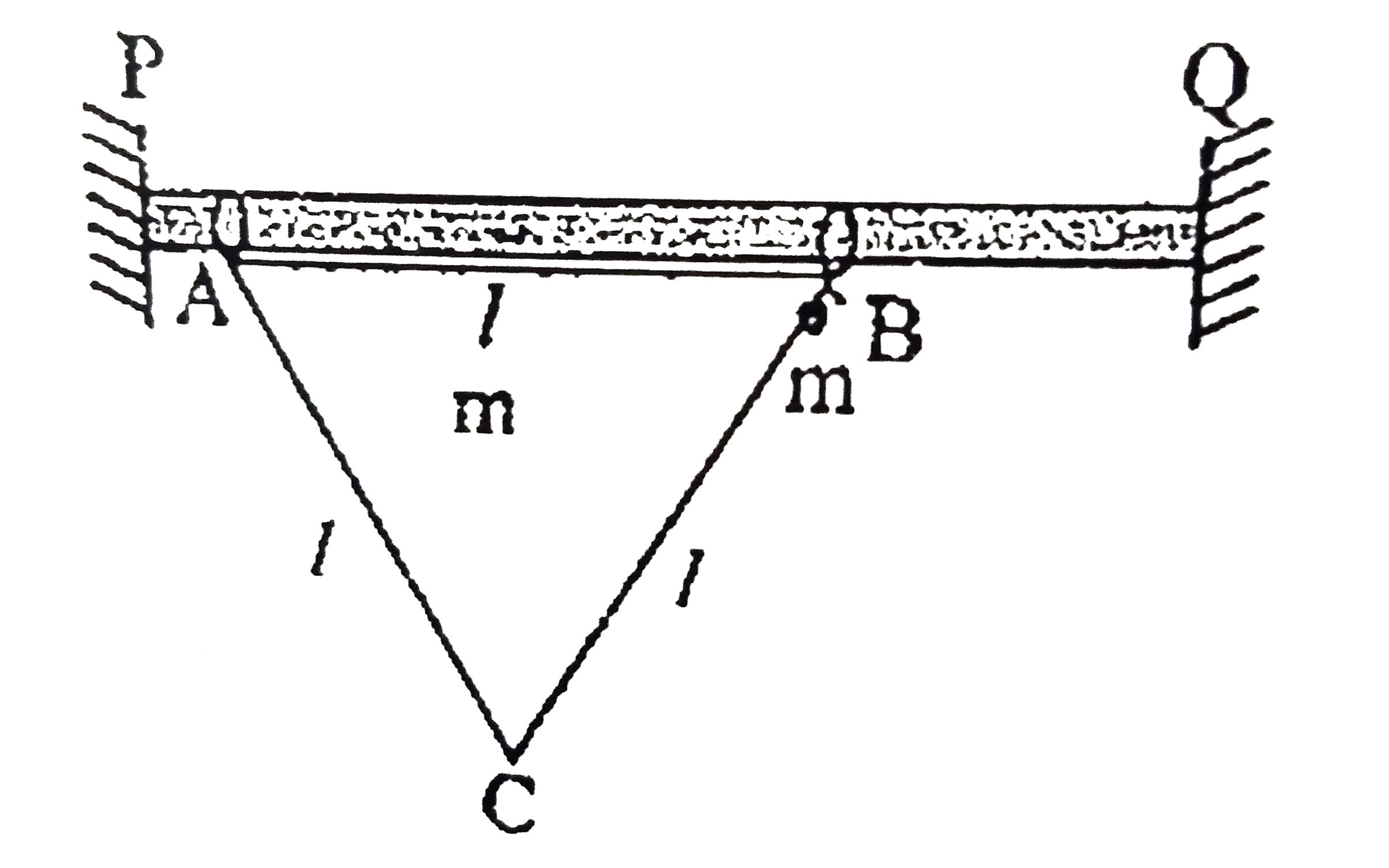
View SolutionA vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
View SolutionA thin but rigid semicircular wire frame of radius r is hinged at O and can rotate in its own vertical plane. A smooth peg P starts from O and moves horizontally with constant speed v0, lifting the frame upward as shown in figure
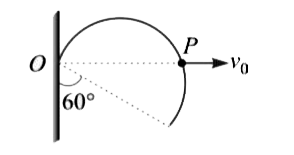
Find the angular velocity ω of the frame when its diameter makes an angle of 60∘ with the vertical :
View Solution
