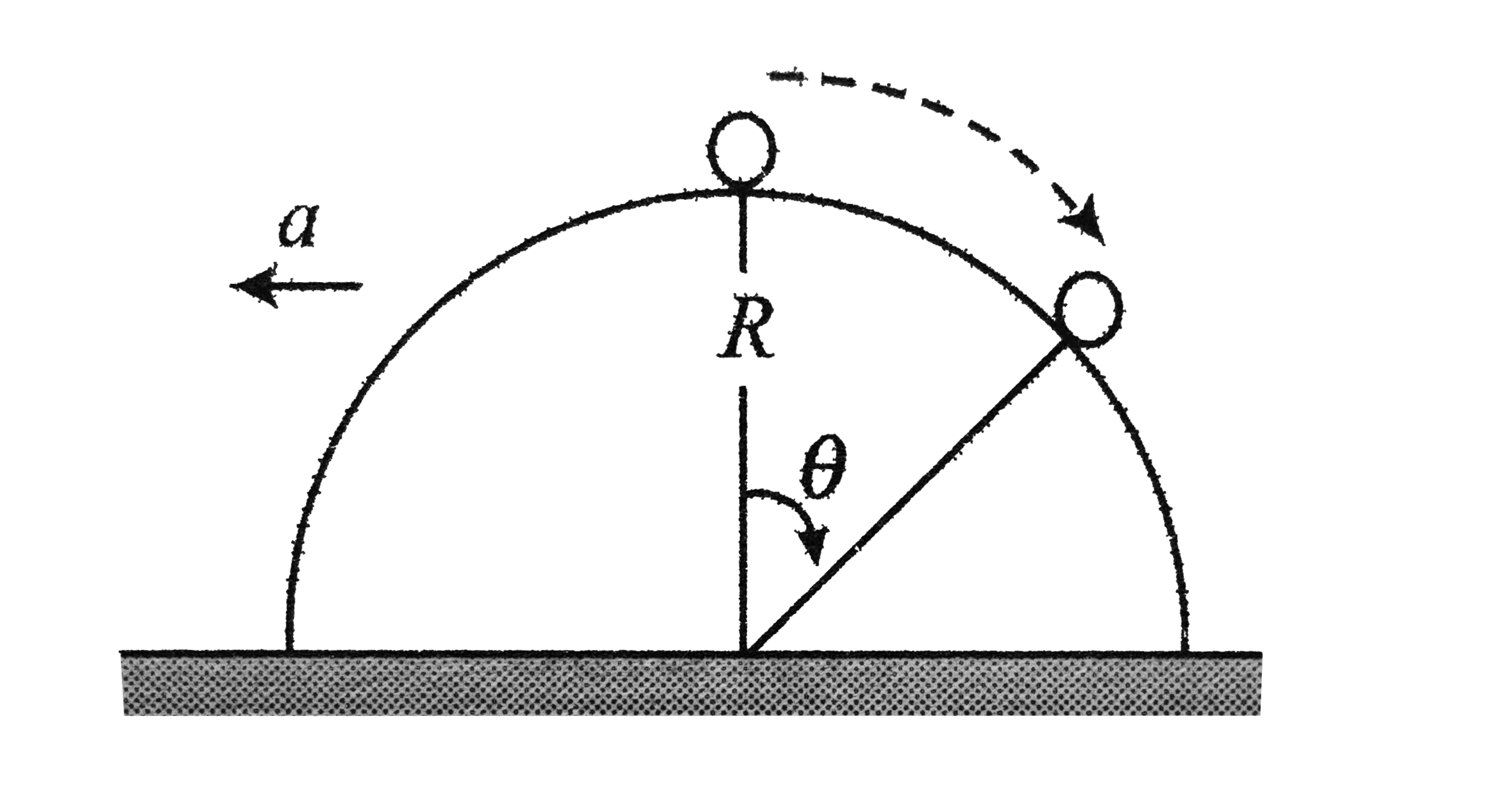
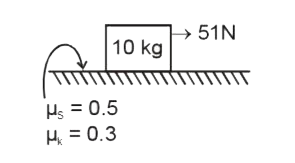A toy truck T at rest, has a hemispherical trough of radius R in it [O is the centre of the hemisphere]. A small block A is kept at the bottom of the trough. The truck is accelerated horizontally with an acceleration a. (i) Find the minimum value of a for which the block is able to move out of the trolley. (ii) If magnitude of a is twice the minimum value found in (i), find the maximum height (measured from its original level at the bottom of the trough) to which the block will rise.
![A toy truck T at rest, has a hemispherical trough of radius R in it [O is the centre of the hemisphere]. A small block A is kept at the bottom of the trough. The truck is accelerated horizontally with an acceleration a. (i) Find the minimum value of a for which the block is able to move out of the trolley. (ii) If magnitude of a is twice the minimum value found in (i), find the maximum height (measured from its original level at the bottom of the trough) to which the block will rise.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C04_E01_065_Q01.png)
The correct Answer is:(i) amin=g
(ii) 2R
Step by step video, text & image solution for A toy truck T at rest, has a hemispherical trough of radius R in it [O is the centre of the hemisphere]. A small block A is kept at the bottom of the trough. The truck is accelerated horizontally with an acceleration a. (i) Find the minimum value of a for which the block is able to move out of the trolley. (ii) If magnitude of a is twice the minimum value found in (i), find the maximum height (measured from its original level at the bottom of the trough) to which the block will rise. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
Ag(cosθ+μsinθsinθ−μcosθ)Bg(sinθ+μcosθcosθ−μsinθ)Cg(sinθ−μcosθsinθ+μcosθ)Dg(cosθ−μsinθsinθ+μcosθ)A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
 A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]If block B moves towards right with acceleration b, find the net acceleration of block A.
 Abˆi+4bˆjBbˆi+bˆjCbˆi+2bˆjDNone of these
Abˆi+4bˆjBbˆi+bˆjCbˆi+2bˆjDNone of these
Find out acceleration of the block. Initially the block is at rest.
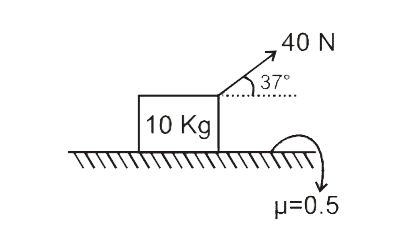
View SolutionFind out the acceleration of the block. If the block is initially at rest.
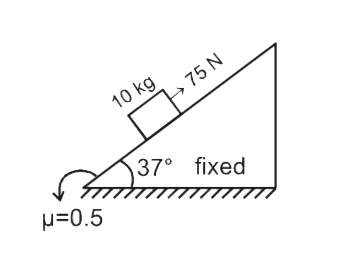
View SolutionFind out minimum acceleration of block A so that the 10 kg block doesn’t fall.
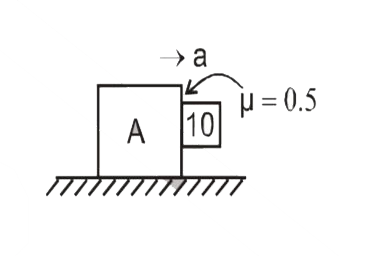
View Solution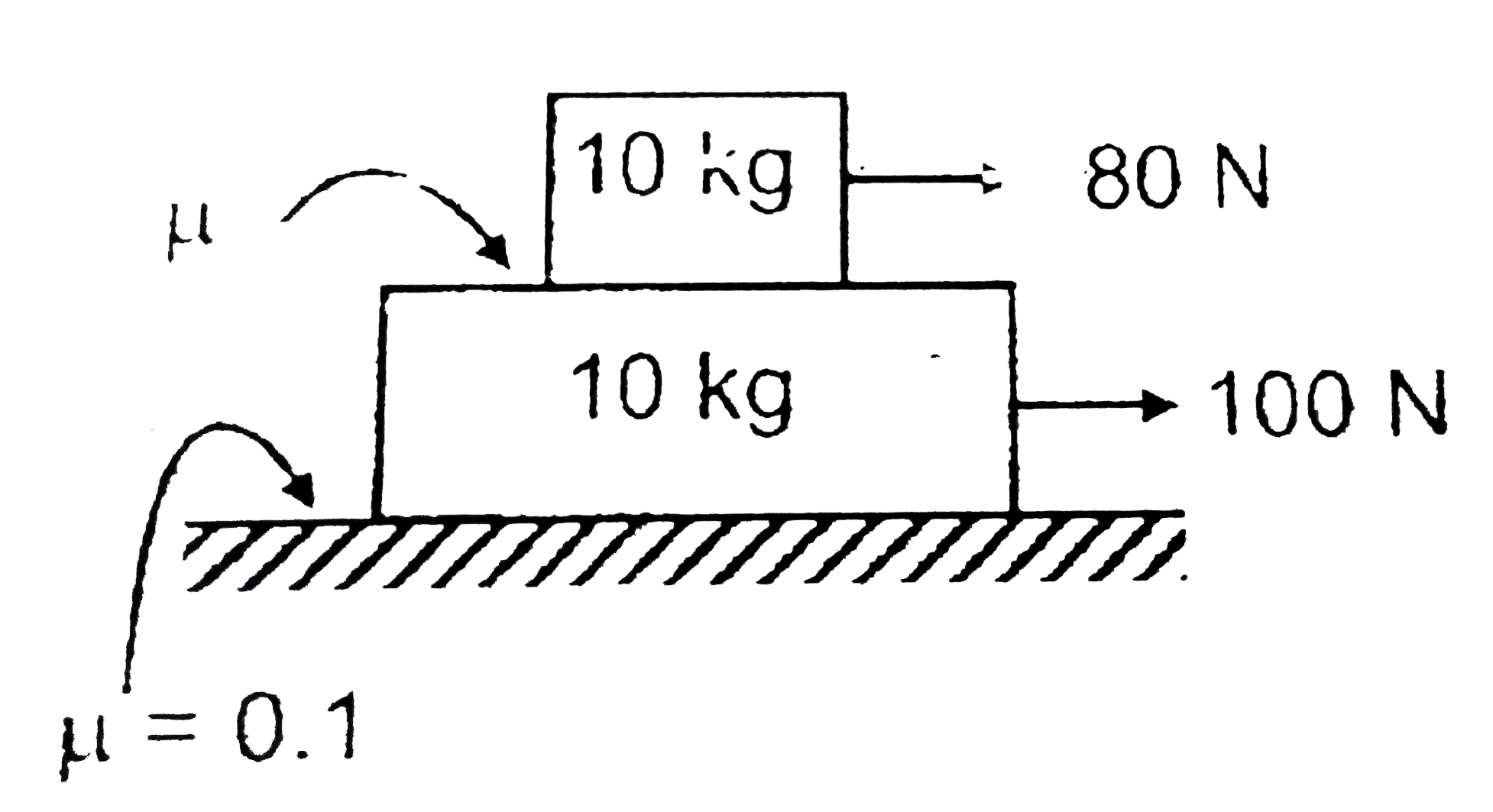
Find minimum μ between the block so that both blocks move with same acceleration.
View SolutionFind the acceleration of block B realtive to the ground if the block A moves to the left with an acceleration a0
 .
.
View Solution