A light thread is tightly wrapped around a fixed disc of radius R. A particle of mass m is tied to the end P of the thread and the vertically hanging part of the string has length πR. The particle is imparted a horizontal velocity V=√4πgR3. The string wraps around the disc as the particle moves up. At the instant the velocity of the particle makes an angle of θ=60∘ with horizontal, calculate.
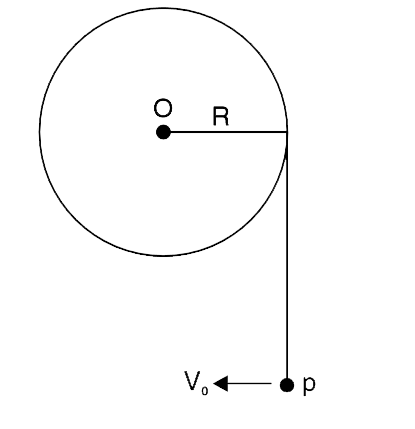
(a) Speed of the particle
(b) Tension in the string
The correct Answer is:(a) √√3gR
(b) mg(√3+12)
Step by step video, text & image solution for A light thread is tightly wrapped around a fixed disc of radius R. A particle of mass m is tied to the end P of the thread and the vertically hanging part of the string has length piR. The particle is imparted a horizontal velocity V=sqrt((4pigR)/3). The string wraps around the disc as the particle moves up. At the instant the velocity of the particle makes an angle of theta=60^(@) with horizontal, calculate. (a) Speed of the particle (b) Tension in the string by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View Solution
Knowledge Check
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
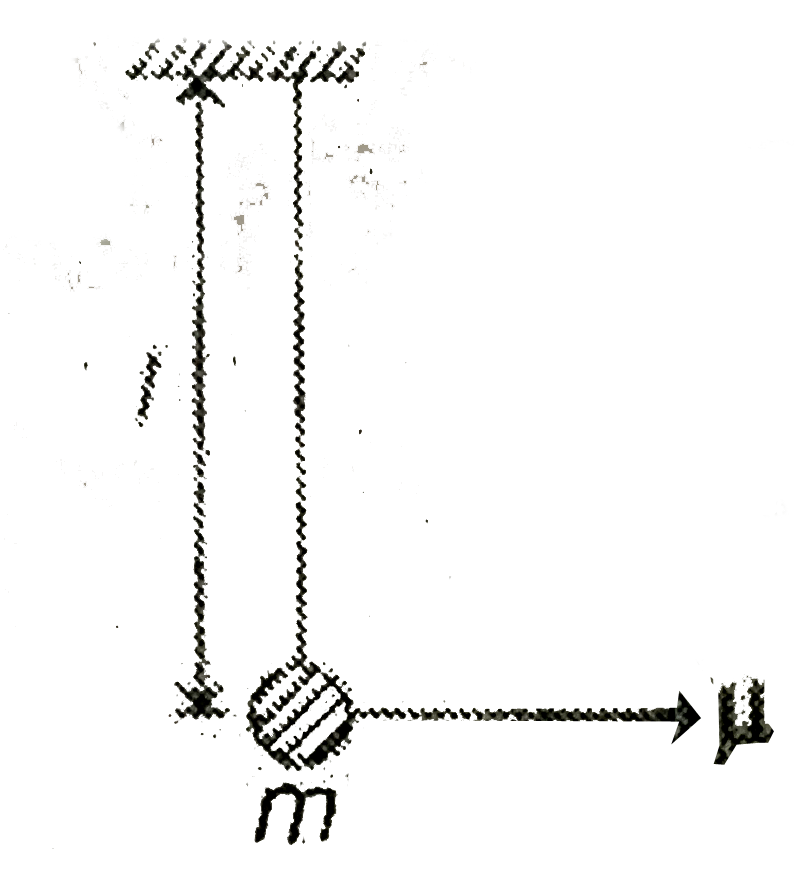
The tension in the string at an instant when acceleration of the particle is horizontal and √3g isAmgB2 mgC4 mgD6 mgA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√TmlA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
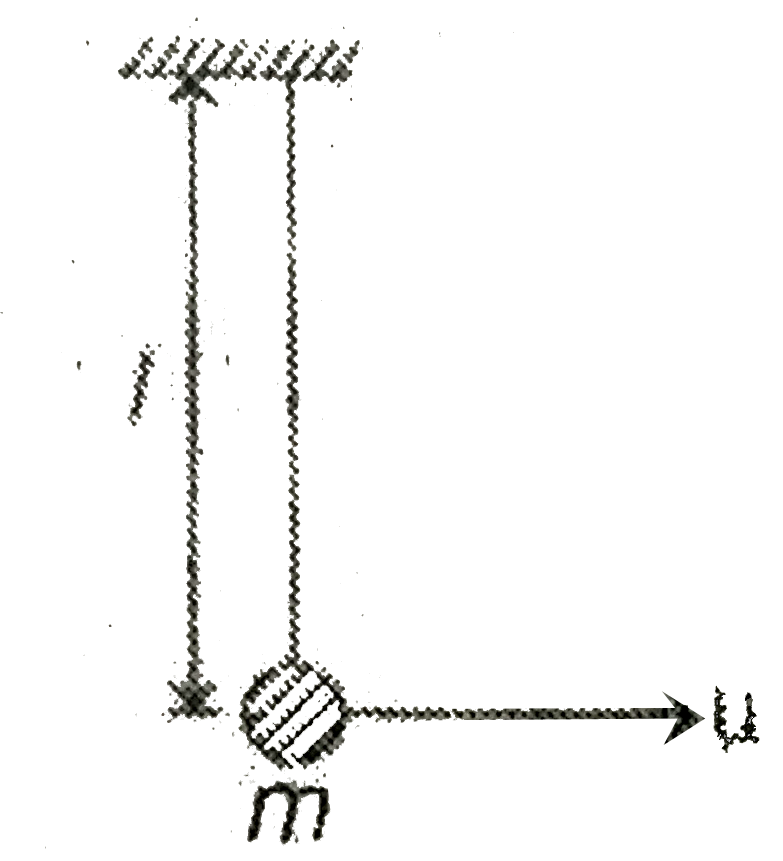
The maximum angle made by the string with downward vertical isAcos−1(14)Bsin−1(14)Cπ2+cos−1(14)Dπ−cos−1(14)
A particle of mass m projected horizontally with velocity u. if it makes an angle θ with the horizontal after some time, then at that instant, its be Broglie wavelength is
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View SolutionA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
View SolutionA particle of mass 'm' is projected from ground with velocity u making angle θ with the vertical. The de-Broglie wave length of the particle at the highest point is:
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View Solution
