A small block is placed on the top of a smooth inverted hemispherical bowl of radius R.
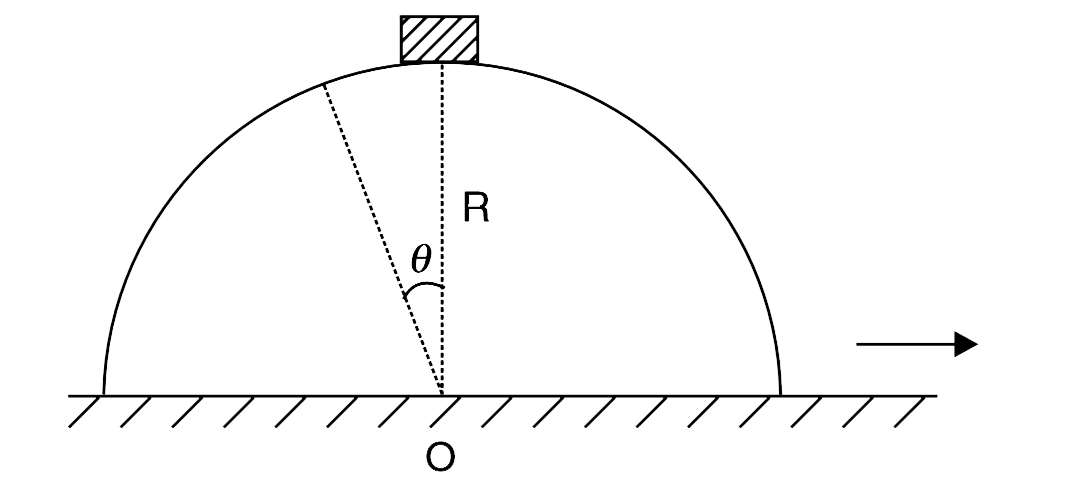
(a) The bowl is given a sudden impulse so that it begins moving horizontally with speed V. Find minimum value of V so that the block immediately loses contact with the bowl as it begins to move. (b) The bowl is given a constant acceleration ‘a’ in horizontal direction. Find maximum value of ‘a’ so that the block does not lose contact with the bowl by the time it rotates through an angle θ=1∘ relative to the bowl. You can make suitable mathematical approximations justified for small value of angle θ.
The correct Answer is:(a) √Rg
(b) 60gπ
Step by step video, text & image solution for A small block is placed on the top of a smooth inverted hemispherical bowl of radius R. (a) The bowl is given a sudden impulse so that it begins moving horizontally with speed V. Find minimum value of V so that the block immediately loses contact with the bowl as it begins to move. (b) The bowl is given a constant acceleration ‘a’ in horizontal direction. Find maximum value of ‘a’ so that the block does not lose contact with the bowl by the time it rotates through an angle theta=1^(@) relative to the bowl. You can make suitable mathematical approximations justified for small value of angle theta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
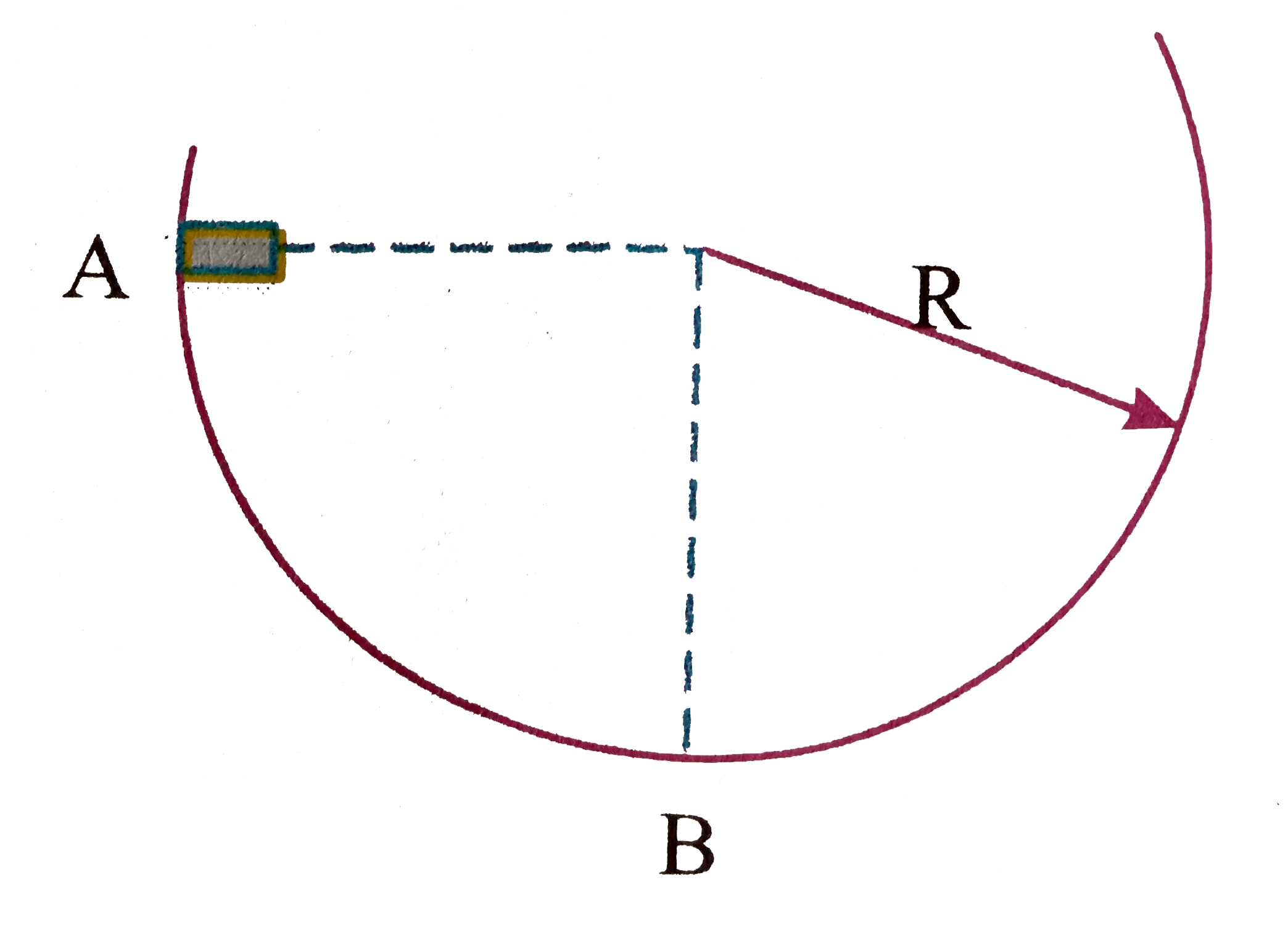
A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at BA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
 Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at BA small ball is pushed from a height h along a smooth hemispherical bowl of rodius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
A√2ghB√2g(R+h)C√2g(R−h)DNone of these
A particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionFigure shows a body A at the top of a frictionless hemispherical inverted bowl of radius R. If the body starts slipping from the highest point, then the horizontal distance between the point where it leaves contact with sphere and the point at which the body was placed is
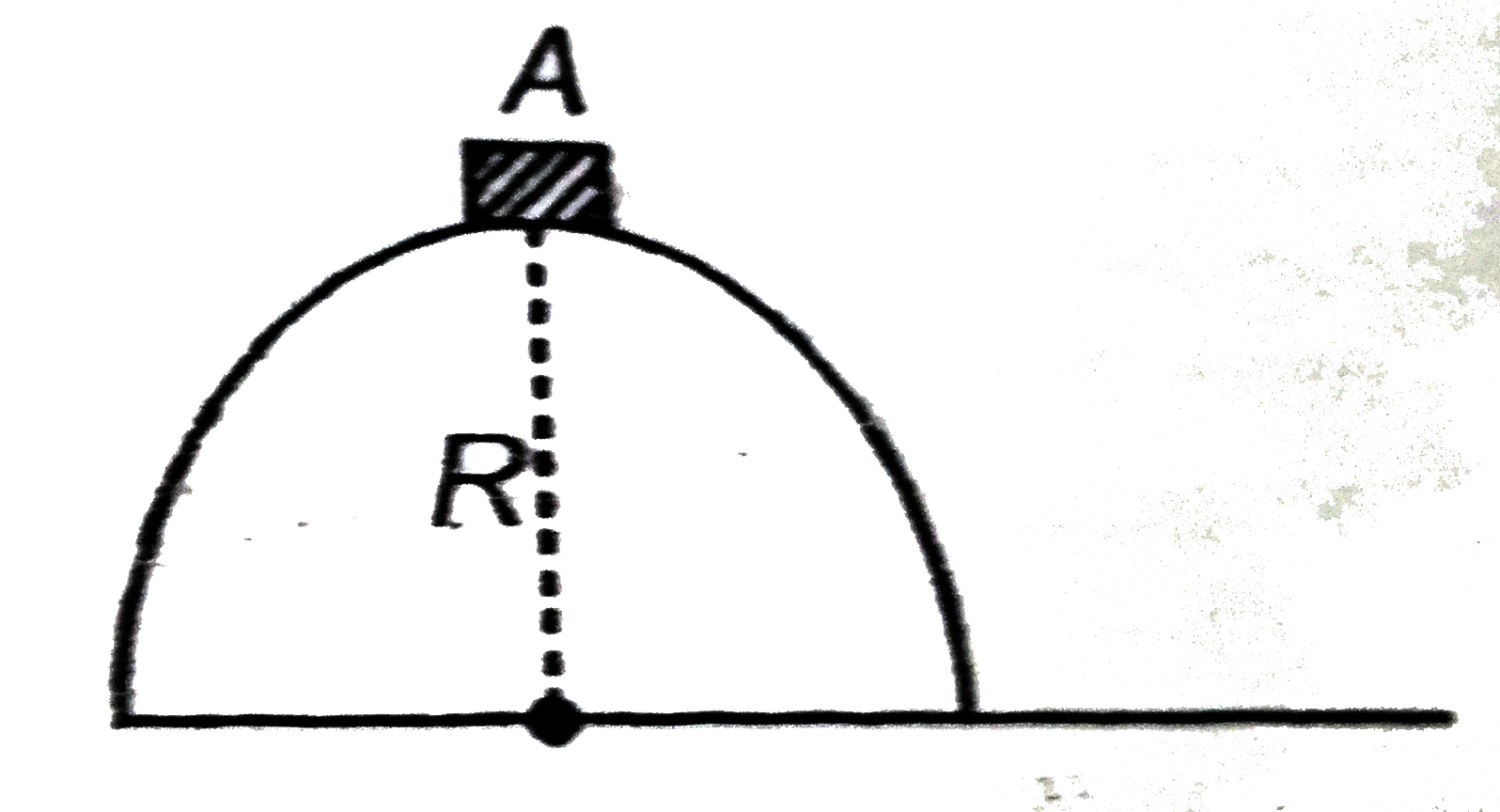
View SolutionA small block of mass m is released from rest from point A inside a smooth hemisphere bowl of radius R, which is fixed on group such that OA is horizontal. The ratio (x) of magnitude of centripetal force and normal reaction on the block at any point B varies with θ as :

View SolutionThe radius of a hemispherical bowl is 6 cm. The capacity of the bowl is
(Take π=227)
View SolutionConsider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
What si the maximum possible value of v so that block does not lose contact with the sphere at the top point ?
View Solution
