A uniform solid sphere of mass M and radius R is rotating with respect to its diameter, with a constant angular velocity ω in free space (i.e., there is no one to exert any force on sphere). Consider an hemispherical part of the sphere (such that axis of rotation lies in the place dividing the sphere in two hemisphere). Net force on this hemisphere due to another hemisphere is nMω2R16. Here n is an integer. Find n
Video Solution
Text Solution
The correct Answer is:3
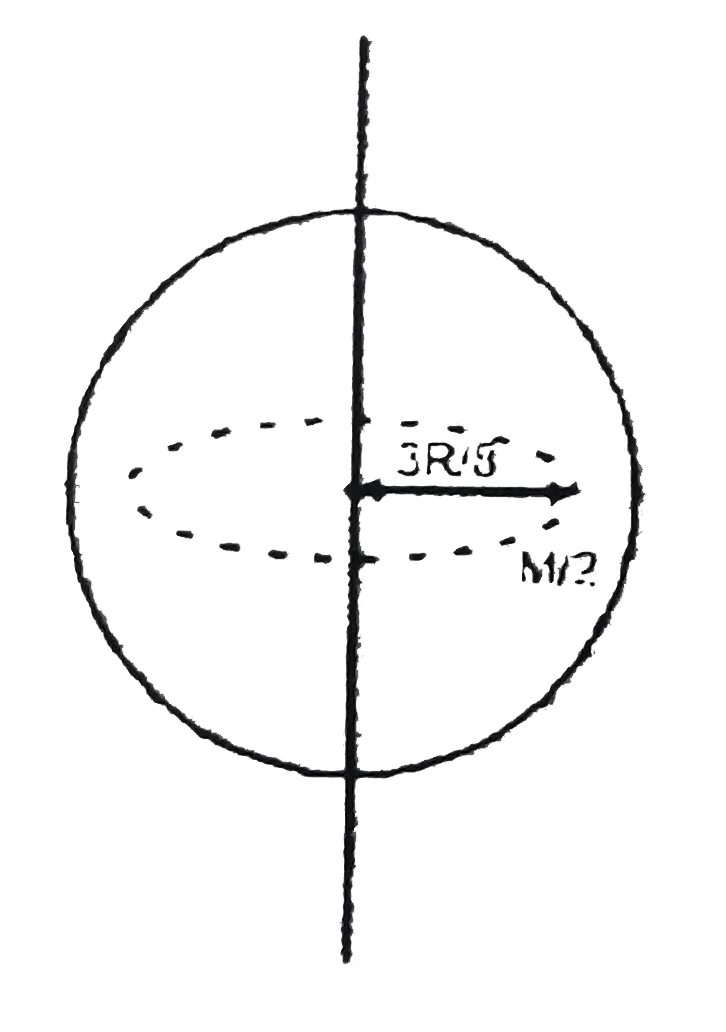
F=M2ω2(3R8)
F=3Mω2R16
|
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
Knowledge Check
If a uniform solid sphere of diameter 0.2 m and mass 10 kg is rotated about its diameter with an angular velocity of 2 rad/s, then the its angular momentum in kg m2/s will be
A0.01B0.02C0.08D0.04A hollow sphere and solid sphere of the same radius rotate about their diameters with the same angular velocity and angular momentum. Then the ratio of their masses is
A3:8B5:8C3:5D5:3A sphere and a hemisphere have the same volume. The ratio of their radii is
A1:2B1:8C1:√2D1:3√2
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionIf the radius of a sphere is equal to the diameter of a hemisphere. Find the ratio of volume of sphere to that of the hemisphere.
View SolutionThe volume of a hemisphere is four times that of a sphere. Find the ratio of the radius of the hemisphere to that of the sphere.
View SolutionRadius of hemisphere is twice that of a sphere. What is the ratio of total surface area of hemisphere and sphere ?
View SolutionRadius of hemisphere is thrice than that of a sphere. What is the ratio of total surface area of hemisphere to that of sphere?
View Solution
