
The kinetic energy of a uniform rod of mass m rotating with constant angular velocit ω about one of its end which is fixed as shown in figure is mω2l2N find N
The correct Answer is:6
dm=dxlm
dE=12dmv2=12dxlm(wx)2
dE=mw22lx2.dx
E=∫dE=mw22l∫l0x2.dx
E=mw2l26
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
Find total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity ω , about a vertical axis XX', shown in figure .

View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View Solution
Knowledge Check
The kinetic energy of an object rotating about a fixed axis with angular momentum L=Iω can be written as.
AK=L2/2IBK=2l2/ICK=L2/IDK=√2L2/IAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
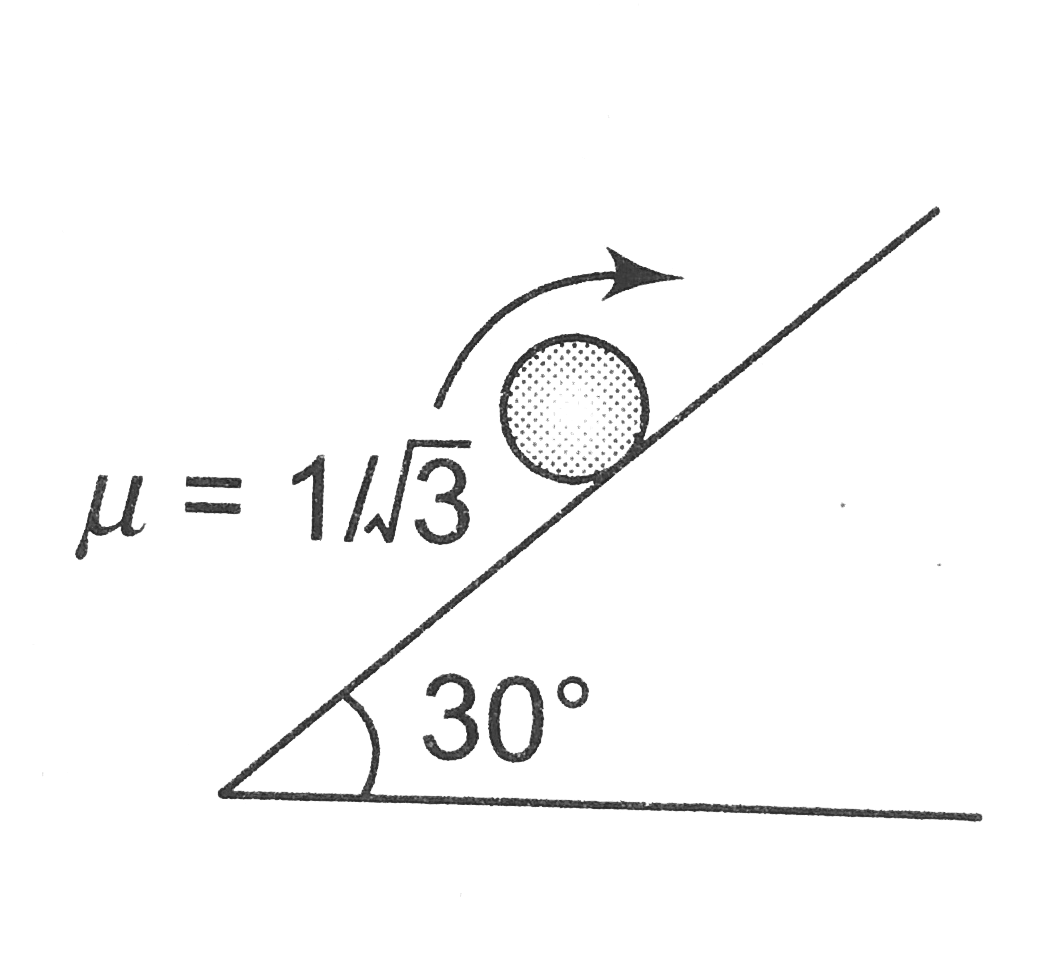 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.A thin uniform copper rod length l and mass m rotates unifomly with an angular velocity ω about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is σmax, cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions

The maximum angular velocity with which the rod can rotate so that is won't break, isA√2σmaxAmlB√2σmaxA3mlC√σmaxA2mlD√3σmaxAml
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
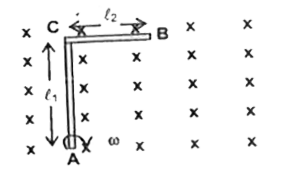
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View SolutionA uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png)
View Solution
