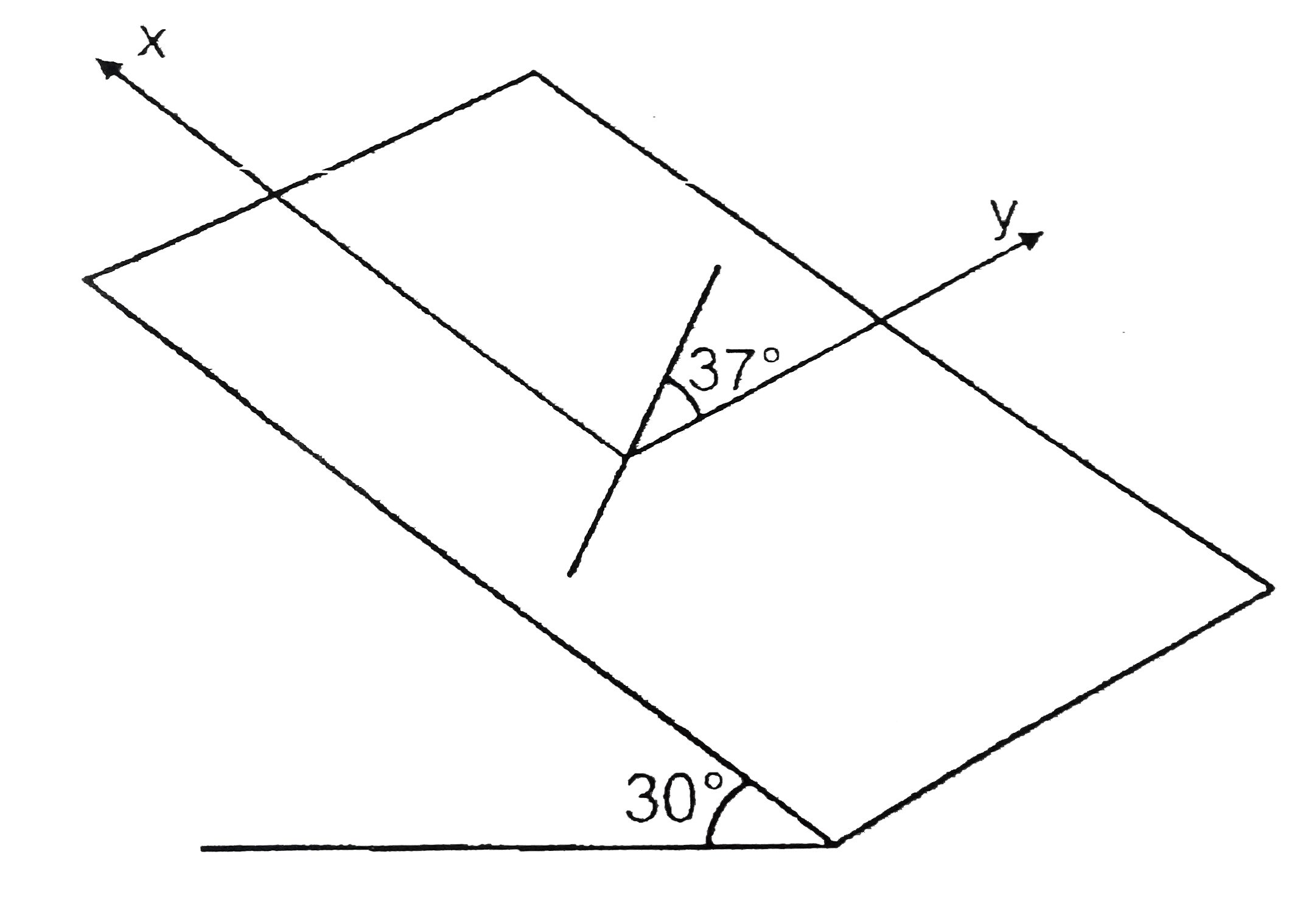
A small sphere is projected with velocity 5ms in a direction 37∘ from the horizontal y-axis on a smoother inclined plane. The motion of sphere takes plane in x-y plane. Magnitude of its velocity after 2 s is:
√65
√55
√36
√45
The correct Answer is:A
vy=5cos37∘=5×45=4ms
vx=usin37∘−(gsin30∘)×t
v=√v2x+v2y=√49+16=√65
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
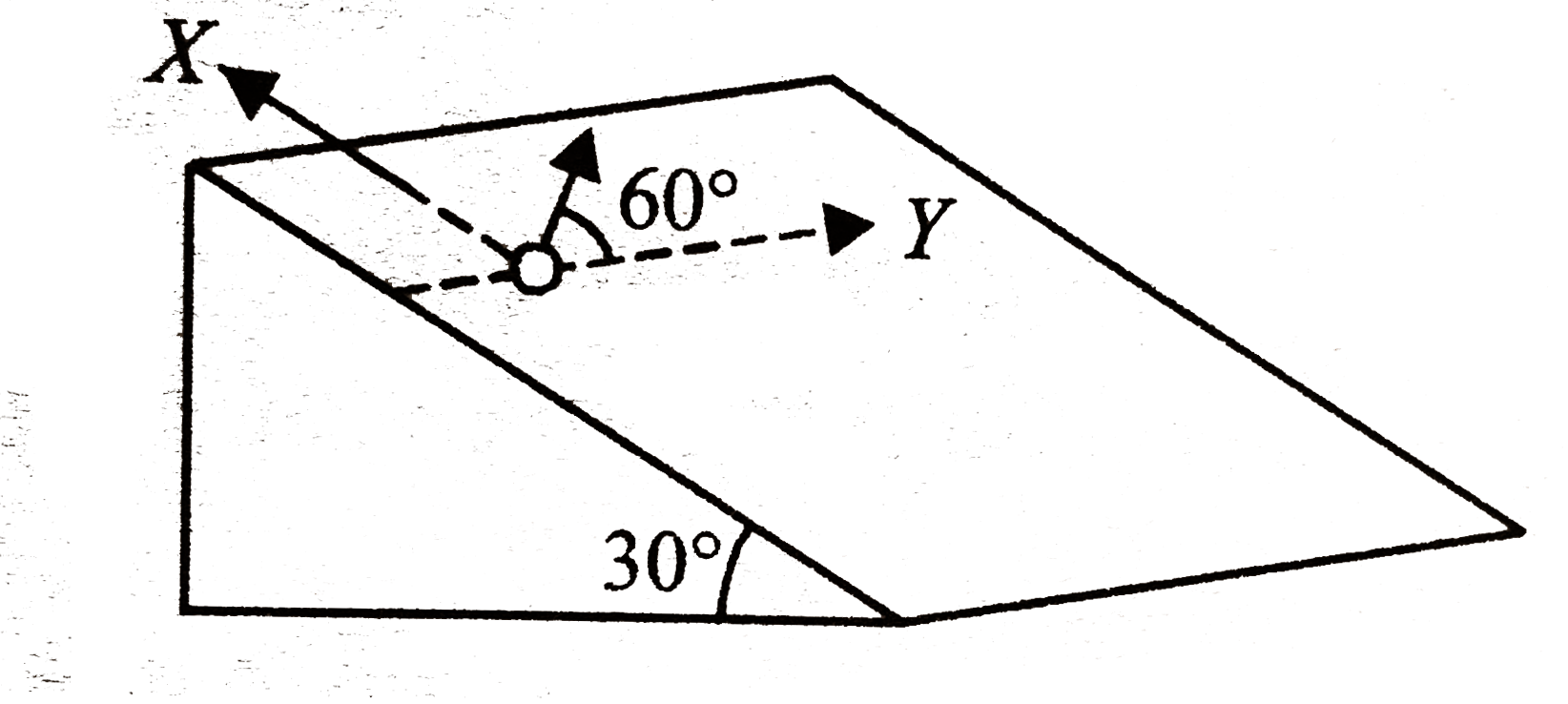
A small sphere is projected with a velocity of 3ms−1 in a direction 60∘ from the horizontal y - axis, on the smooth inclined plane (Fig. 5.197). The motion of sphere takes place in the x - y plane. Calculate the magnitude v of its velocity after 2s.
 .
.
View SolutionA small marble is projected with a velocity of 10m/s in a direction 45∘from the y-direction on the smooth inclined plane. Calculate the magnitude v of its velocity of after 2s (Take g=10m/s2)

View Solution
Knowledge Check
A particle is projected up with a velocity of v0=10m/s at an angle of θ0=60∘ with horizontal onto an inclined plane. The angle of inclination of the plane is 30∘. The time of flight of the particle till it strikes the plane is (take g=10ms−2)
A1sB1/2sC2√3sD12√3sA particle is projected with velocity 10m/s at an angle of 45∘ with the horizontal from some height. Consider point of projection as origin and motion in xy plane. Then (→g=10ˆjm/s2)
AIts velocity after √2 sec will be perpendicular to its initial velocityBIts velocity after √3 sec will be perpendicular to its initial velocityCIts radius of curvature is 40m at x=5(√3+1) mDIts radius of curvature is 5m at x=5mA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3)
A particle is projected from ground with velocity 50m/s at 37∘ from horizontal. Find velocity and displacement after 2 s. sin37∘=35.
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. u
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. h
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solution