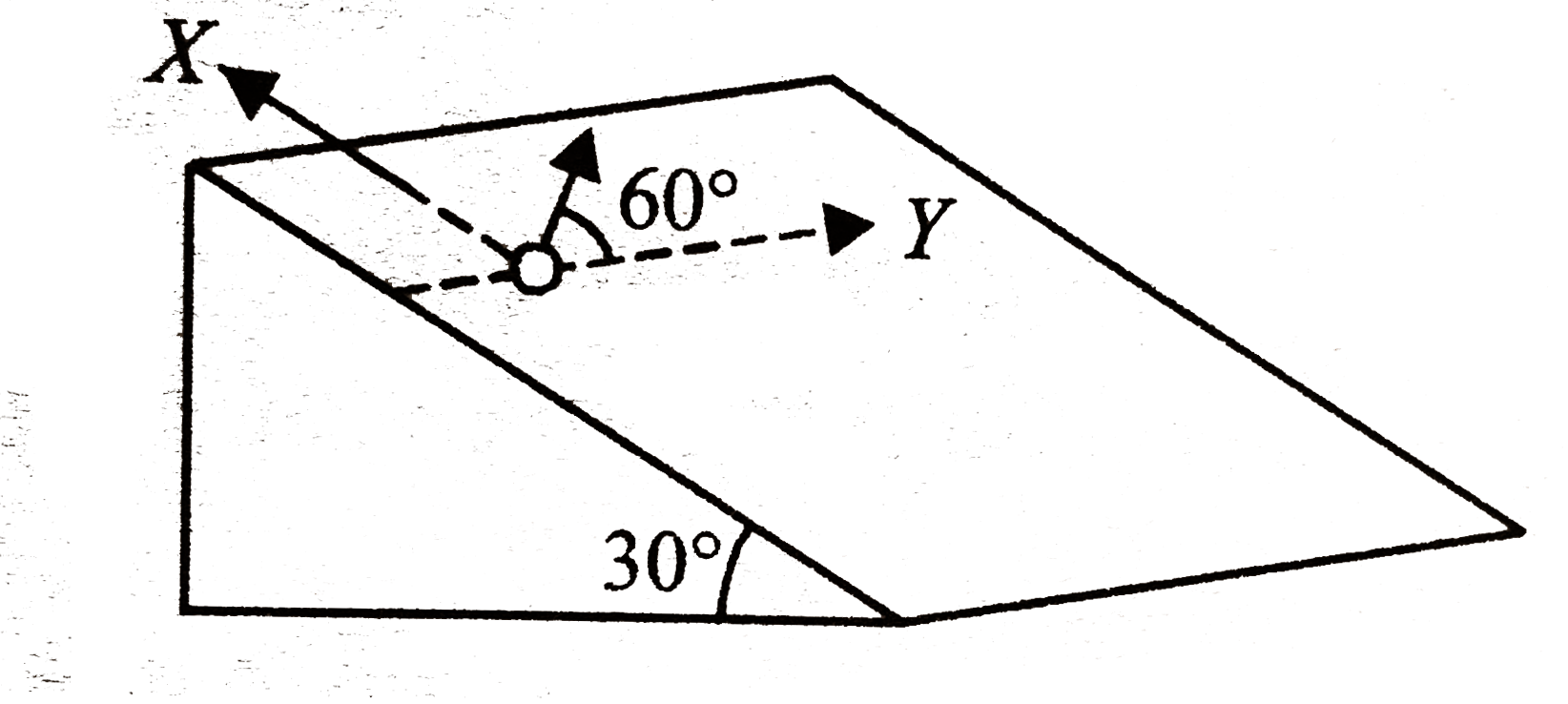
A small sphere is projected with a velocity of $3 m s^{- 1}$ in a direction $60^{\circ}$ from the horizontal y - axis, on the smooth inclined plane (Fig. 5.197). The motion of sphere takes place in the x - y plane. Calculate the magnitude $v$ of its velocity after $2 s$ .
.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $1.5 m s^{- 1}$

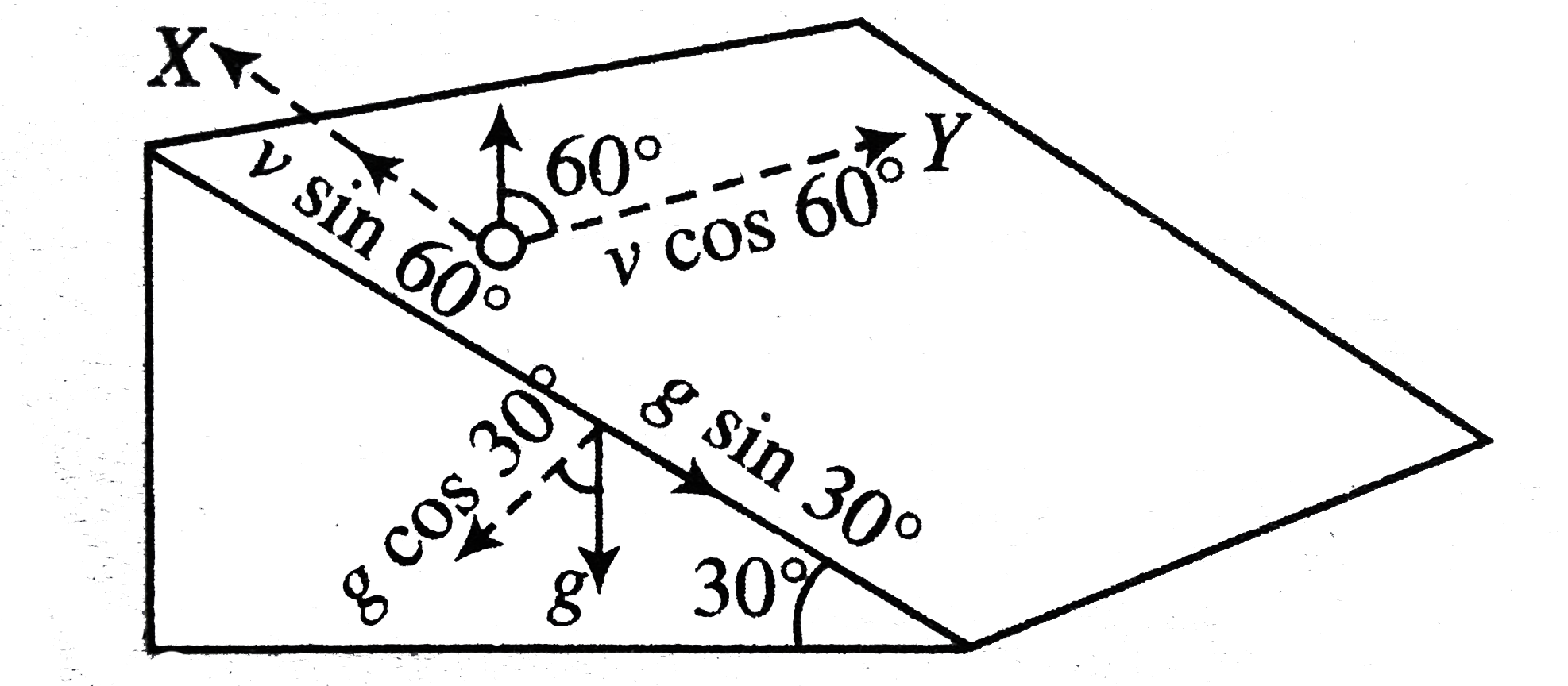
The motion of the sphere takes place in a plane , the x - and x - components of its acceleration are $A_{x} = - g {sin 30}^{\circ}$ , $a_{y} = 0$ The x- and y - components of the sphere's velocity at time $t = 2 s$ are
$V_{x} = v_{0 x} - a_{x} t = 3 {sin 60}^{\circ} - g {sin 30}^{\circ} \times 2 = 0.1 m s^{- 1}$
$V_{y} = v {cos 60}^{\circ} = c o n s tan t = 1.5 m s^{- 1}$
So the magnitude of sphere's velocity is
$| \to v | = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{{(0.1)}^{2} + {(1.5)}^{2}} ≅ 1.5 m s^{- 1}$
.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

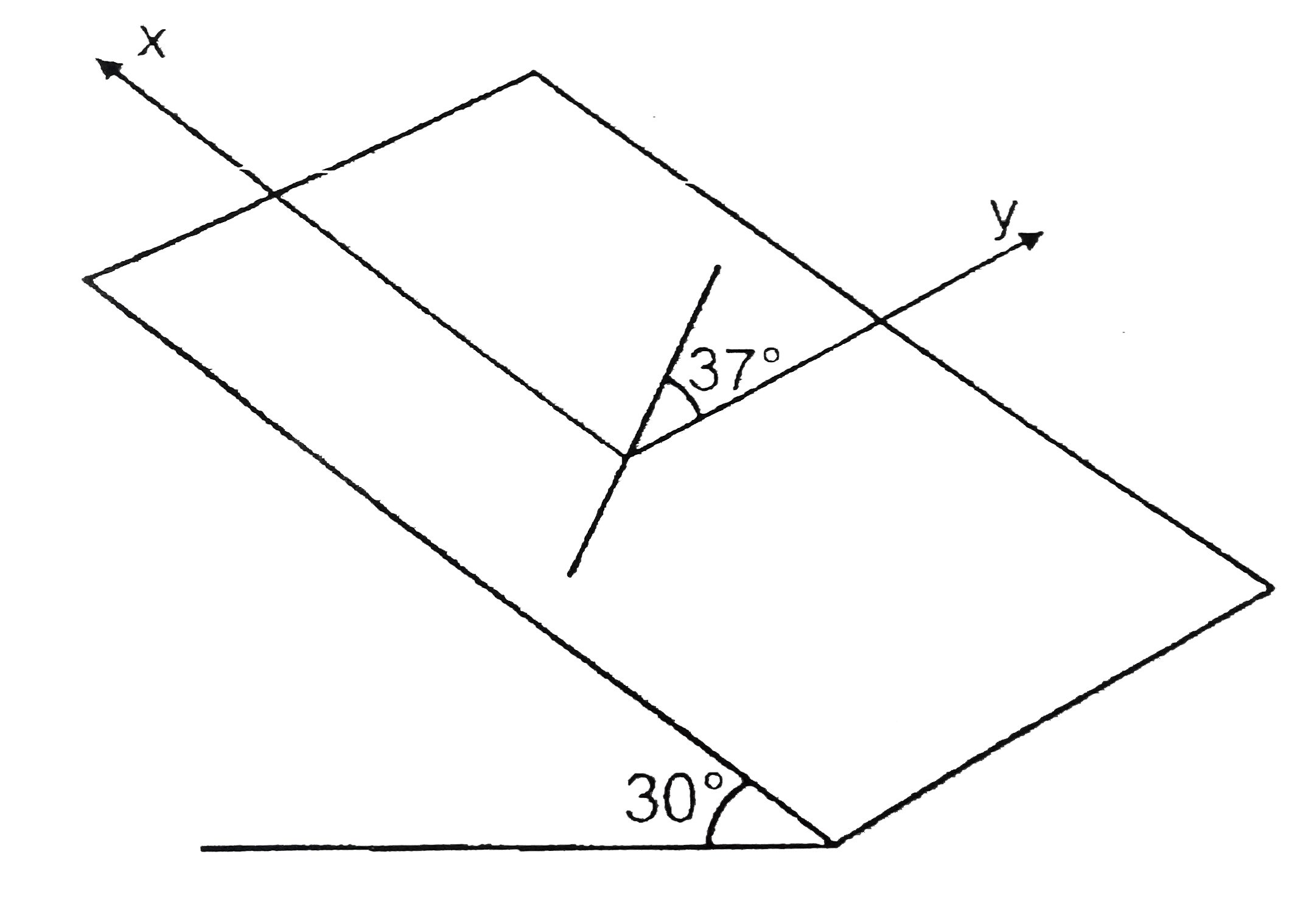
A small sphere is projected with velocity $5 \frac{m}{s}$ in a direction $37^{\circ}$ from the horizontal y-axis on a smoother inclined plane. The motion of sphere takes plane in x-y plane. Magnitude of its velocity after 2 s is:
A $\sqrt{65}$
B $\sqrt{55}$
C $\sqrt{36}$
D $\sqrt{45}$
Question 2 - Select One
A body is projected with a velocity of $20 m s^{- 1}$ in a direction making an angle of $60^{\circ}$ with the horizontal. Determine its (i) position after 0.5 s and (ii) the velocity after $0.5 s$ .
A $15 m$ , $7.43 m$ , $10 m s^{- 1}$ , $12.42 m s^{- 1}$
B $5 m$ , $6.43 m$ , $10 m s^{- 1}$ , $12.42 m s^{- 1}$
C $5 m$ , $7.43 m$ , $10 m s^{- 1}$ , $12.42 m s^{- 1}$
D $15 m$ , $7.43 m$ , $10 m s^{- 1}$ , $1.42 m s^{- 1}$
Question 3 - Select One
A particle is projected with a velocity of $20 m s^{- 1}$ at an angle of $60^{\circ}$ to the horizontal. The particle hits the horizontal plane again during its journey. What will be the time of impact ?
A $3.53 s$
B $2.4 s$
C $1.7 s$
D1s

CENGAGE PHYSICS-KINEMATICS-2-Exercise Subjective

Home
Ask Doubt
Profile