A ship A streams due north at 16kmh−1 and a ship B due west at 12kmh−1. At a certain instant B is 10km north east of A. Find the
(a) magnitude of velocity of Arelative→B.
(b) nearest distance of approach of ships.
The correct Answer is:(a) 20kmh−1 ;
(b) √2km
To solve the problem, we need to find the relative velocity of ship A with respect to ship B and the nearest distance of approach of the ships.
1. Determine the velocity vectors:
- Ship A's velocity vector can be represented as:
→VA=0^i+16^jkm/h
- Ship B's velocity vector can be represented as:
→VB=−12^i+0^jkm/h
2. Calculate the relative velocity of A with respect to B:
→VAB=→VA−→VB=(0^i+16^j)−(−12^i+0^j)=12^i+16^jkm/h
3. Find the magnitude of the relative velocity:
|→VAB|=√(12)2+(16)2=√144+256=√400=20km/h
(b) Nearest Distance of Approach of Ships
1. Determine the angle of the relative velocity:
- The angle α can be calculated using:
tanα=1612=43
- Therefore, α=tan−1(43).
2. Calculate the distance of closest approach:
- The initial distance d between the ships is 10km at an angle of 45∘ (northeast).
- The nearest distance D can be calculated using the formula:
D=d⋅sinα
- Where d=10km and sinα=45 (from the triangle formed by the velocities).
3. Substituting the values:
D=10⋅45=8km
4. Calculate the perpendicular distance:
- The perpendicular distance from the path of A to the initial position of B can be calculated using:
Dmin=10⋅cos(45∘)−10⋅sin(45∘)⋅1220
- Simplifying gives us:
Dmin=10⋅1√2−10⋅45⋅1√2=10√2−8√2=2√2=√2km
Final Answers:
- (a) The magnitude of the velocity of A relative to B is 20km/h.
- (b) The nearest distance of approach of the ships is 2km.
- Ship A's velocity vector can be represented as:
→VA=0^i+16^jkm/h
- Ship B's velocity vector can be represented as:
→VB=−12^i+0^jkm/h
→VAB=→VA−→VB=(0^i+16^j)−(−12^i+0^j)=12^i+16^jkm/h
|→VAB|=√(12)2+(16)2=√144+256=√400=20km/h
- The angle α can be calculated using:
tanα=1612=43
- Therefore, α=tan−1(43).
- The initial distance d between the ships is 10km at an angle of 45∘ (northeast).
- The nearest distance D can be calculated using the formula:
D=d⋅sinα
- Where d=10km and sinα=45 (from the triangle formed by the velocities).
D=10⋅45=8km
- The perpendicular distance from the path of A to the initial position of B can be calculated using:
Dmin=10⋅cos(45∘)−10⋅sin(45∘)⋅1220
- Simplifying gives us:
Dmin=10⋅1√2−10⋅45⋅1√2=10√2−8√2=2√2=√2km
- (a) The magnitude of the velocity of A relative to B is 20km/h.
- (b) The nearest distance of approach of the ships is 2km.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Single Correct
Explore 76 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.4
Explore 11 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A motor boat is racing towards North at 25km/h and the water current in that region is 10km/h in the direction of 6000 East of South. Find the resultant velocity of the boat.
View SolutionA ship is streaming due West at 12ms−10. A boy runs across the dech at 5ms−1 in a direction at right angles to the direction of motion of the ship towards South, Calculate the velocity of the boy relative to ship.
View Solution
Knowledge Check
A car A going north-east at 80km/h and another car B is going south-east at 60km/h. The direction of the velocity of A relative to B makes an angle with the north equal to:
Atan−1(2/7)Btan−1(7/2)Ctan−1(7)Dtan−1(1/7)A bird is flying towards north with a velocity 40kmh−1 and a train is moving with velocity 40kmh−1 towards east. What is the velocity of the bird boted by a man in the train ?
A40√2kmh−1N−EB40√2kmh−1S−EC40√2kmh−1N−WD40√2kmh−1S−WA ship is travelling due north at 40 kmph. The captain of the finds that a second ship is always sailing 60∘ west of north at a speed of 40 kmph. The velocity of the second ship then must be
A40 kmph, 30∘ west of northB40 kmph. 60∘ west of southC40√3 kmph, 30∘ west of northD40√3 kmph, 60∘ west of south
A verticle is moving due north with an absolute velocity 54km/h. An observer at P is at distance 30m to the west of the line of travel. What is the angular velocity of vehicle relative to the observer at t=0 and t=2s.
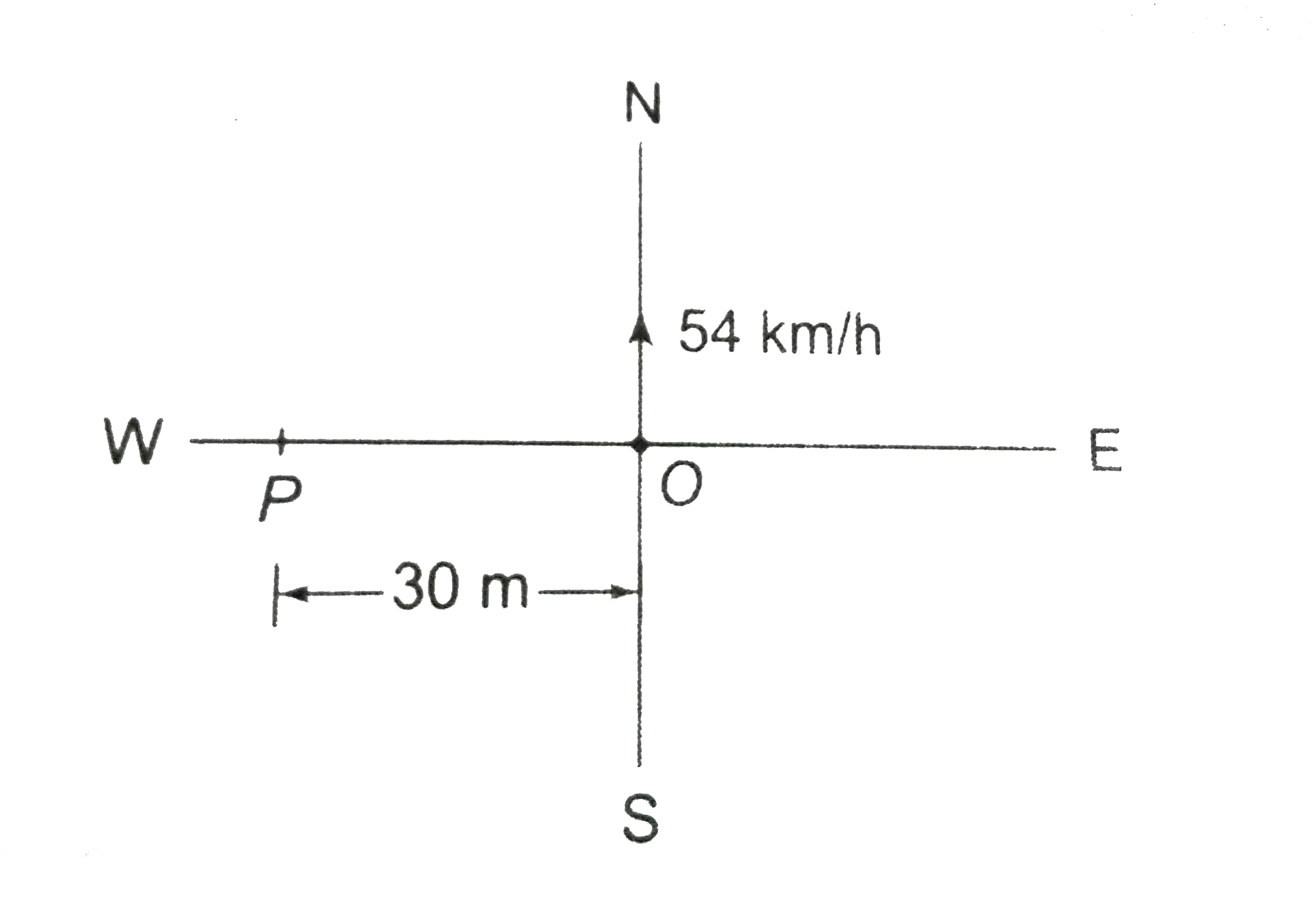
View SolutionShip A is located 4.0 km north and 2.5 km east of ship B. Ship A has a velocity of 22 km/h toward the south, and ship B has a velocity of 40 km/h in a direction 37∘ north of east. (a) What is the velocity of A relative to B in unit-vector notation with toward the east? (b) Write an expression (in terms of ˆiandˆj) for the position of A relative to B as a function of t, where t = 0 when the ships are in the positions described above. ( c) At what time is the separation between the ships least? (d) What is that least separation?
View SolutionTwo ships, A and B, leave port at the same time. Ship A travels northwest at 24 knots, and ship B travels at 28 knots in a direction 40∘ west of south (1 knot = 1 nautical mile per hour, see Appendix D). What are the (a) magnitude and (b) direction of the velocity of ship A relative to B? ( c) After what time will the ships be 160 nautical miles apart? (d) What will be the bearing of B (the direction of B's position) relative to A at that time?
View SolutionA ship is sailing due north at a speed of 1.25ms−1. The current is taking it towards east at the rate of 2ms−1. and a sailor is climbing a vertical pole in the ship at the rate of 0.25ms−1. Find the magnitude of the velocity of the sailor with respect to ground.
View SolutionThe velocity of a body is 100kmh−1, 30^(@) west of south . Find the north ad east components of the vector.
View Solution

