A ball is projected for maximum range with speed 20ms−1. A boy is located at a distance 25m from point of throwing start run to catch the ball at the time when the ball was projected. Find the speed of the boy so that he can catch the ball (Takeg=10ms−1).
The correct Answer is:5.3ms−1
R=202sin(2×45∘)10=40mT=2×20sin45∘10=2(√2)s
x=40−15=15m
Required speed =152√2=5.3ms−1.
 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Single Correct
Explore 76 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.4
Explore 11 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A ball is projected from ground with a speed of 20ms−1 at an angle of 45∘ with horizontal.There is a wall of 25m height at a distance of 10m from the projection point. The ball will hit the wall at a height of
View SolutionA ball is projected vertically up wards with a velocity of 100 m/s. Find the speed of the ball at half the maximum height. (g=10m/s2)
View Solution
Knowledge Check
A ball is projected form ground with a speed of 20 ms^(-1)
A5mB7.5mC10mD12.5mA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
AIt covers a distance of 5 m in 2nd second of its motionBThe displacement in 2nd and 3rd second are equalCThe distance covered in 2nd and 3rd second are equalDThe average speed for first 4 seconds is zeroThe maximum height attained by a ball projected with speed 20ms−1 at an angle 45∘ with the horizontal is [take g = 10ms−2]
A40 mB20 mC10 mD30 m
A person can throw a ball to a maximum horizontal distance of 90.m Calculat the maximum vertcal heitht to which he can through the ball. Fiven g=10ms−2.
View SolutionA football is kicked with speed 20ms−1 at a projection angle of 45∘ from the ground. A receiver on the goal line 20m away in the disrection of the kich runs the same instant to meet the ball. What must he his speed, of he is to catch the ball cefore it hits the ground ? Take g=10ms−2.
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

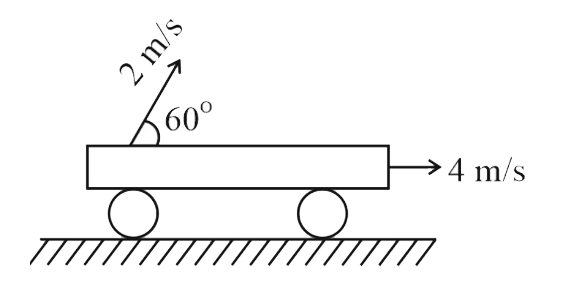
View SolutionA ball is projected with a speed of 2ms−1 with respect to a trolley which is moving with 4ms−1, as shown in the figure. The angle at which ball is projected with respect to the horizontal in ground frame is
View SolutionA ball is projected from a high tower with speed 20 m/s at an angle 30∘ with horizontal x-axis. The x-coordinate of the ball at the instant when the velocity of the ball becomes perpendicular to the velocity of projection will be (take point of projection as origin):
View Solution

