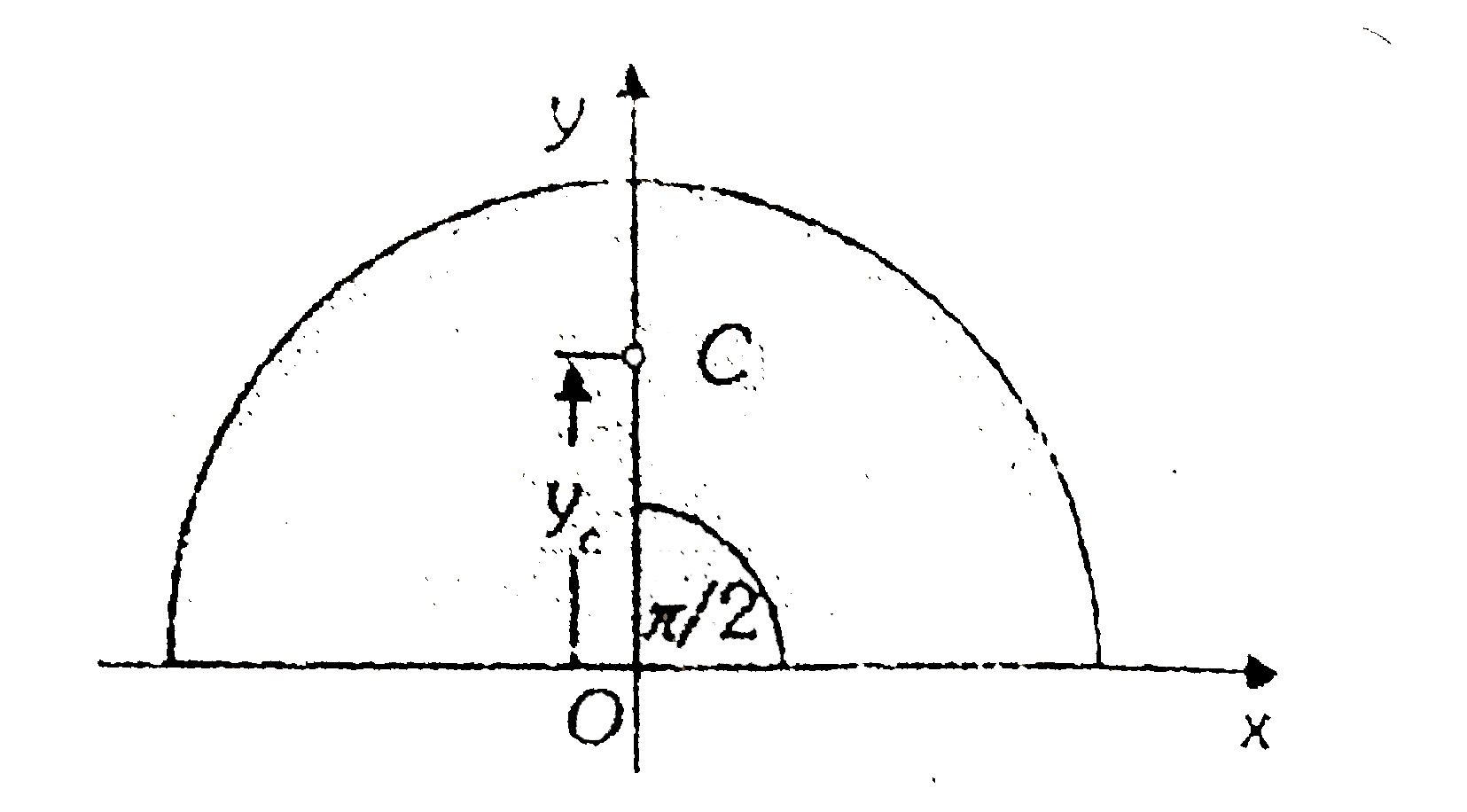
Find coordinates of mass center of a uniform semicircular plate of rad

Find the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R

A $(\frac{4 R}{3 π}, 0)$
B $(\frac{2 R}{π + 2}, 0)$
C $(\frac{2 R}{π}, 0)$
D $(\frac{R}{π + 2}, 0)$
Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
A $\frac{M L^{2}}{3}$
B $\frac{2 M L^{2}}{3}$
C $\frac{M L^{2}}{6}$
D $M L^{2}$
Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
A $\frac{M L^{2}}{3}$
B $\frac{2 M L^{2}}{3}$
C $\frac{2 M L^{2}}{6}$
D $M L^{2}$

Find coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.