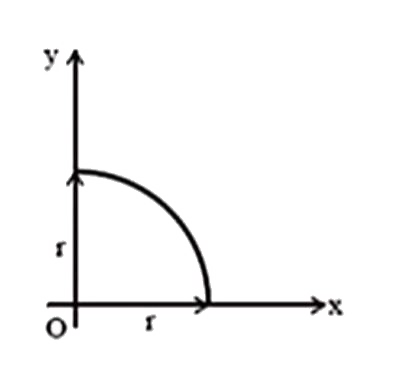
Find coordinates of mass center of a quarter ring of radius r placed in the first quadrant of a Cartesian coordinate system, with centre at origin.

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the coordinates of the center of mass of a quarter ring of radius $r$ placed in the first quadrant of a Cartesian coordinate system with the center at the origin, we can follow these steps:
Step 1: Understand the Geometry
The quarter ring is a circular arc that spans an angle of $\frac{π}{2}$ radians (or 90 degrees) and is located in the first quadrant. The center of the quarter ring is at the origin (0, 0).
Step 2: Determine the Angle
For a quarter ring, the angle subtended at the center is $\frac{π}{2}$ . Therefore, the angle $θ$ we will use in our calculations is $\frac{π}{4}$ because the angle $2 θ$ is equal to $\frac{π}{2}$ .
Step 3: Calculate the Distance to the Center of Mass
The distance from the center (origin) to the center of mass $C$ of the quarter ring can be calculated using the formula:
$O C = \frac{R sin (θ)}{θ}$
Substituting $R = r$ and $θ = \frac{π}{4}$ :
$O C = \frac{r sin (\frac{π}{4})}{\frac{π}{4}} = \frac{r \cdot \frac{\sqrt{2}}{2}}{\frac{π}{4}} = \frac{r \sqrt{2}}{2} \cdot \frac{4}{π} = \frac{2 r \sqrt{2}}{π}$
Step 4: Determine the Coordinates
Since the center of mass of the quarter ring lies at an angle of $45^{\circ}$ (or $\frac{π}{4}$ ), we can find the coordinates $(x, y)$ of the center of mass using:
$x = O C cos (\frac{π}{4}) and y = O C sin (\frac{π}{4})$
Substituting $O C$ :
$x = \frac{2 r \sqrt{2}}{π} \cdot cos (\frac{π}{4}) = \frac{2 r \sqrt{2}}{π} \cdot \frac{\sqrt{2}}{2} = \frac{2 r}{π}$
$y = \frac{2 r \sqrt{2}}{π} \cdot sin (\frac{π}{4}) = \frac{2 r \sqrt{2}}{π} \cdot \frac{\sqrt{2}}{2} = \frac{2 r}{π}$
Step 5: Final Coordinates
Thus, the coordinates of the center of mass of the quarter ring are:
$(\frac{2 r}{π}, \frac{2 r}{π})$

Updated on:7/8/2024

Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
A $\frac{M L^{2}}{3}$
B $\frac{2 M L^{2}}{3}$
C $\frac{M L^{2}}{6}$
D $M L^{2}$
Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
A $\frac{M L^{2}}{3}$
B $\frac{2 M L^{2}}{3}$
C $\frac{2 M L^{2}}{6}$
D $M L^{2}$
Find the x coordinate of the centre of mass of the bricks shown in figure :

A $\frac{24}{25} l$
B $\frac{25}{24} l$
C $\frac{15}{16} l$
D $\frac{16}{15}$