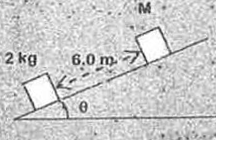
Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
![Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m//s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m//s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M. [Take sintheta=tantheta=0.05 and g=10m//s^2]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V02_CH11_E01_193_Q01.png)
The correct Answer is:e=0.84,M=15.21kg
For body of mass m from A to B u=10m/s (given)
a=−[mgsinθ+fm]=−[mgsinθ+μmgcosθm]
=−[gsinθ+μgcosθ]=−g[sinθ+μcosθ]
=−10[0.05+0.25×0.99]
=−2.99m/s2
v2−u2=2as
⇒v=√100+2−(−2.99)×6=8m/s
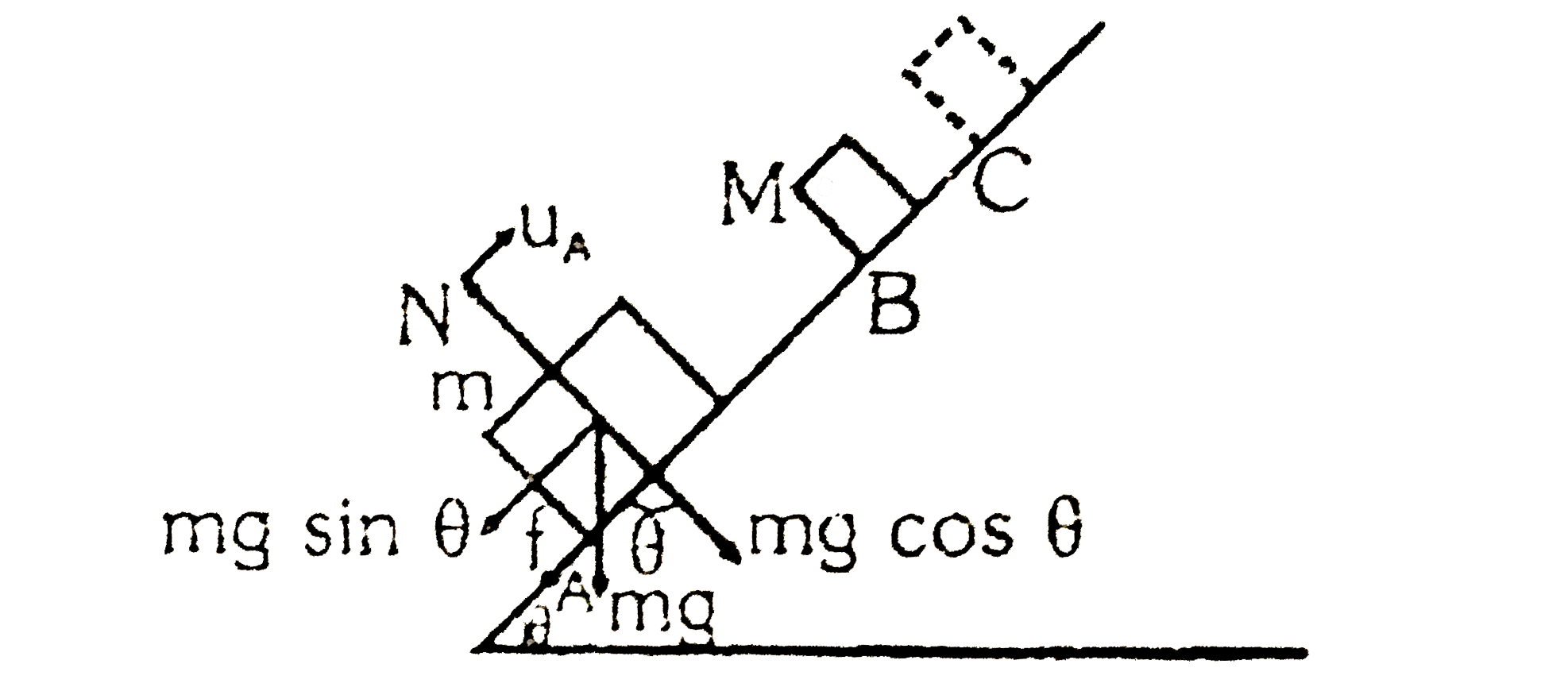
After collision
Let v1 be the velocity of mass m after collision. Body v2 be the velocity of mass M after collision. Body of mass M moving from B to C and Coming to rest.
u=v2,v=0 a=−2.99m/s2
and s=0.5 v2−u2=2as
⇒(0)2=v22=2(−2.99)×0.5
⇒v22=1.73m/s
Body of mass m mocing from B to A after collision
u=v1,v=+1m/s
(K.E.+P.E.)initial=(K.E.+P.E.)final+Wfrication
12mv21+mgh=12mv2+0+μgs
12v21+10×(6×0.05)=12(1)2+0.25×10×6
v1=−5m/s
sinθ=h6
h=6sinθ=6×0.05

∴ Coefficient of restituation
e=∣∣∣Relative velocity of sepaerationRelative velocity of approach∣∣∣
=∣∣∣−5−1.738−0∣∣∣=0.84
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V A
Explore 20 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
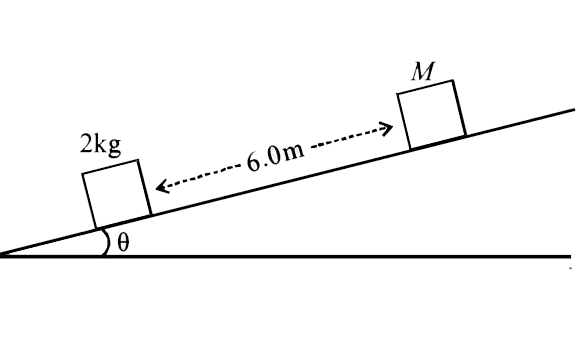
Two block of mass 2 kg and M kg are at rest on an inclined plane and are separated by a distance of 6.0 m as a showm in figure. The coefficient of friction between each of the blocks and the inclined plane is 0.25. The 2 kg block is given a velocity of 10.0 m/s up the inclined plans. It collides with M, comes back and has a velocity of 10 m/s when it reaches its initial position. The other block of mass M after the collision moves 0.5 m up and comes to rest. Calculate the coefficient of restitution between the 2 kg block and the mass M.
[Take sinθ≈tanθ=0.5,cosθ=1 and g=10m/sec2]
View SolutionTwo blocks of mass 2 kg and M are at rest as an inclined plane and are sparated of by a distance of 6.0 m as shown in figure . The coefficient of friction between each of the block and the inclined plane is 0.25 . The 2 kg block is given a velocity of 10.0 m//s up the inclined plate if collied with M comes back and has a velocity of 1.0m//s when if rached its inital position , The ofter block M ofter the collisiin its resitition . THe ofter the colition its 0.5 m up and come to rest caleslate the coefficient of resttuion between the block and the mass of the block M [Take sin theta +n tan theta = 0.05anda = 10m//s^(2)]
View Solution
Knowledge Check
In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8NA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθ
A block of mass 0.5 kg has an initial velocity of 10ms−1 down an inclined plane of angle 30∘, the coefficient of friction between the block and the inclined surface is 0.2. The velocity of the block after it travels a distance of 10 m is
View SolutionTwo blocks of masses 4 kg and 2 kg are in contact with each other on an inclined plane of inclination 30∘ as shown in the figure . The coefficient of friction between 4 kg mass and the inclined plane is 0.3 , whereas between 2 kg mass and the plane is 0.2 . find the contact force between the blocks .

View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution

