Two blocks of masses 4 kg and 2 kg are in contact with each other on an inclined plane of inclination 30∘ as shown in the figure . The coefficient of friction between 4 kg mass and the inclined plane is 0.3 , whereas between 2 kg mass and the plane is 0.2 . find the contact force between the blocks .

The acceleration of 4 kg mass
If θ=30∘,μk=0.3
a4=g(sinθ−μkcosθ)
=10[12−0.3×√32]=2.6ms−2
The acceleration of 2 kg mass
a2=10[12−0.2×√32]=3.27ms−2
∴ a2>a4
Thus , there will be contact force between the blocks and they move together . if 'a' is the common acceleration ,
(m1−m2)a=(m1+m2)gsinθ−(μ1m1+μ2m2)gcosθ
6a=6×10×12−(0.3×4+0.2×2)×10×√32
6a=30−13.856
⇒ a=2.7ms−2
For , 4 kg mass , mg sin θ+fconstant−ffriction=ma
4×10×12+fc−0.3×10×10×√32=4×2.7
fc=10.8+10.4−20
∴ fc=1.2N
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Problem For Practice
Explore 23 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:OBJECTIVE QUESTIONS ( only one choice is correct )
Explore 80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
Two block of masses 2kg and 4kg are released from rest over a smooth inclined place of inclination 30∘ as shown in figure what is the normal force between the two blocks?

View SolutionTwo masses 6 kg and 4 kg are connected by a flexible inextensible string rest on an inclined plane inclined at 60∘ with the horizontal as shown in figure. The coefficient of friction between the plane and the 6kg mass is 0.1 and the between the plane and the 4 kg massis 0.6 .
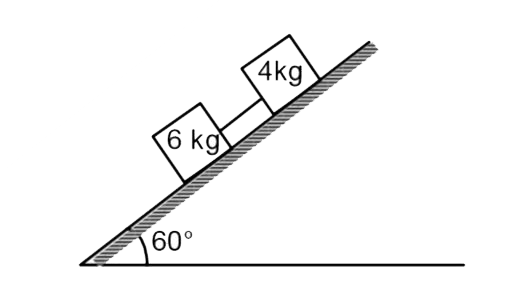
Find the tension in the connecting string.
View Solution
Knowledge Check
A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
Amgsinθ√1+μ2B√(mgsinθ)2+(μmgcosθ)2CmgsinθDmgA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5N
In Fig. 6-52, two blocks, in contact, slide down an inclined plane AC of inclination 30∘ . The coefficient of kinetic friction between the 2.0 kg block and the incline is u1=0.20 and that between the 4.0 kg block and the incline is μ2=0.30. Find the magnitude of the acceleration.

View SolutionA block of mass m=4kg is placed over a rough inclined plane as shown in fig . The coefficient of friction between the block and the plane μ=0.5 A force F=10N is applied on the block at an angle of 30∘. Find the contact force between the block and the plane.
k

View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

View SolutionA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .
.
View SolutionA block of mass m = 4 kg is placed over a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is u=0.5. A force F= 10 N is applied on the block at an angle of 30°. The friction force between the block and wedge is

View Solution