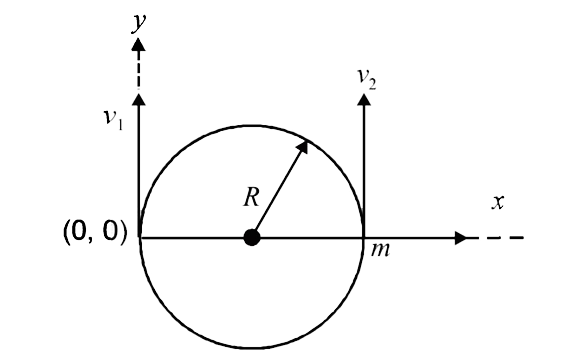
A particle of mass m, moving in a cicular path of radius R with a cons

A particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
AZero
BIndependent of speed
CProportional to radius r
DProportional to $v^{2}$
A particle of mass $m$ is moving along a circle of radius $r$ with a time period $T$ . Its angular momentum is
A $\frac{2 π m r}{T}$
B $\frac{4 π m r}{T}$
C $\frac{2 π m r^{2}}{T}$
D $\frac{4 π m r^{2}}{T}$
A particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
Adistance travelled
Bdisplacement
Caverage speed
Daverage velocity

The correct Answer is: $- m v_{2} \frac{\sin (v_{2})}{R} t \hat{i} + m (v_{2} cos \frac{v_{2}}{R} t - v_{1}) \hat{j}$