Question

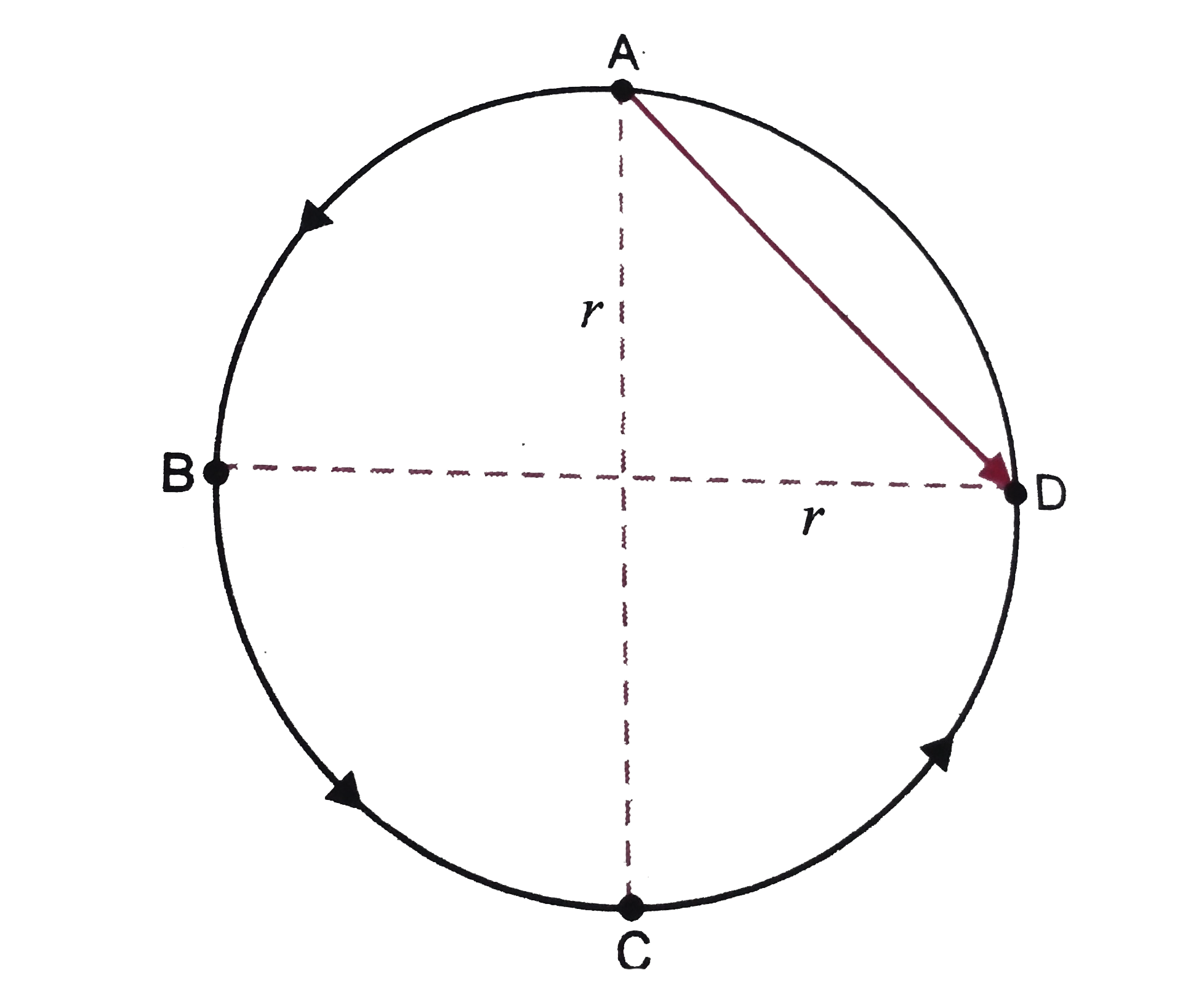
A particle moves along a circle of radius $R$ with a constant angular speed $\omega$ . Its displacement (only magnitude) in time $t$ will be

Options

A. `omega t`
B. `2R cos omega t`
C. `2 R sin omega t`
D. `2R "sin" (omega t)/(2)`

Answer

D

Explanation

To find the magnitude of the displacement of a particle moving along a circle of radius $$R$$ with a constant angular speed $$\omega$$ after a time $$t$$, we can follow these steps:

1. Understand the Motion: The particle moves in a circular path, and we need to determine its displacement after a time \( t \). The displacement is the straight-line distance between the initial and final positions of the particle.

2. Determine the Angular Displacement: The angular displacement \( \theta \) in time \( t \) can be calculated using the formula:
\( \theta = \omega t \)
where \( \omega \) is the angular speed.

3. Draw the Circle: Visualize the circle with radius \( R \). Let the initial position of the particle be point \( A \) and the final position after time \( t \) be point \( B \).

4. Identify the Chord: The straight line connecting points \( A \) and \( B \) represents the displacement. This line is a chord of the circle.

5. Draw the Perpendicular from the Center: From the center of the circle \( O \), draw a perpendicular line to the chord \( AB \). Let this perpendicular meet the chord at point \( O' \). This bisects the chord into two equal segments, \( AO' \) and \( BO' \).

6. Use Right Triangle Properties: In the right triangle \( AOO' \):
- The angle \( AOB \) is \( \theta \).
- The angle \( AO'O \) is \( 90^\circ \).
- The angle \( AOO' \) is \( \frac{\theta}{2} \).

7. Apply the Sine Rule: The length of \( AO' \) can be calculated using the sine function:
\( AO' = R \sin\left(\frac{\theta}{2}\right) \)

8. Calculate the Total Displacement: Since \( AB = AO' + BO' = 2 \cdot AO' \):
\( AB = 2R \sin\left(\frac{\theta}{2}\right) \)

9. Substitute for \( \theta \): Now substitute \( \theta = \omega t \) into the displacement formula:
\( AB = 2R \sin\left(\frac{\omega t}{2}\right) \)

10. Final Result: Thus, the magnitude of the displacement after time \( t \) is:
\( \text{Displacement} = 2R \sin\left(\frac{\omega t}{2}\right) \)

Summary:
The magnitude of the displacement of the particle after time \( t \) is given by:
\( \text{Displacement} = 2R \sin\left(\frac{\omega t}{2}\right) \)