A particle begins to move with a tangential acceleration of constant magnitude 0.6m/s2 in a circular path . If it slips when total acceleration becomes 1m/s2, then the angle through which it would have turned before it stars to slip is :
1/3rad
2/3rad
4/3rad
2rad
The correct Answer is:B
aNet=√a2g+a2c
ω2=ω20+2ωθ
∵ω0=0
so ω2=2αθ
ω2R=2(αRθ)
ac=ω2R=2atθ
1=√0.36+(1.2×θ)2
⇒1−0..36=(1.2θ)2
⇒0.81.2=θ
⇒θ=23radian
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 42
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 43
Explore 11 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 40
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A particle begins to move with a tangential acceleration of constant magnitude 0.6ms2 in a circular path. If it slips when its total acceleration becomes 1ms2, then the angle through which it would have turned before it stảrts to slip is ab radian. Find (ab).
View SolutionA body starts revolving from rest in a circular path of radius 2 m with tangential acceleration a =2tm/s2. If its total acceleration at t=2 sec. is n√5m/s2, then the value of n is:
View Solution
Knowledge Check
A particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
A1/αB√αC1/√αDαA particle starts moving from rest at t=0 with a tangential acceleration of constant magnitude of πm/s2 along a circle of radius 6 m. The value of average acceleration, average velocity and average speed during the first 2√3 s of motion, are respectively :
A3√2m/s2,πm/s,π√3m/sBπm/s2,2√3m/s,π√3m/sCπ√3m/s2,2√3m/s,πm/sDNone of the aboveA particle starting from rest moves with a constant angular acceleration α in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is -
A1αBαC1√αD√α
A particle is moving with a constant angular acceleration of 4rad/s2 in a circular path. At time t=0 , particle was at rest. Find the time at which the magnitudes of centripetal acceleration and tangential acceleration are equal.
View SolutionFind the total acceleration of a particle, moving in a circular track of radius 2 m, with constant angular acceleration of 1 rad/sec2 at time t = 2 seconds from the center
View SolutionA particle is moving with constant angular acceleration (α) in a circular path of radius √3m. At t=0, it was at rest and at t=1s, the magnitude of its acceleration becomes √6ms2, then α (in rads2 ) is
View SolutionA particle starts with constant angular acceleration of 2 rad/s2 in a circle of radius 4m. Find angle between net acceleration and radial acceleration after 2 s :-
View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
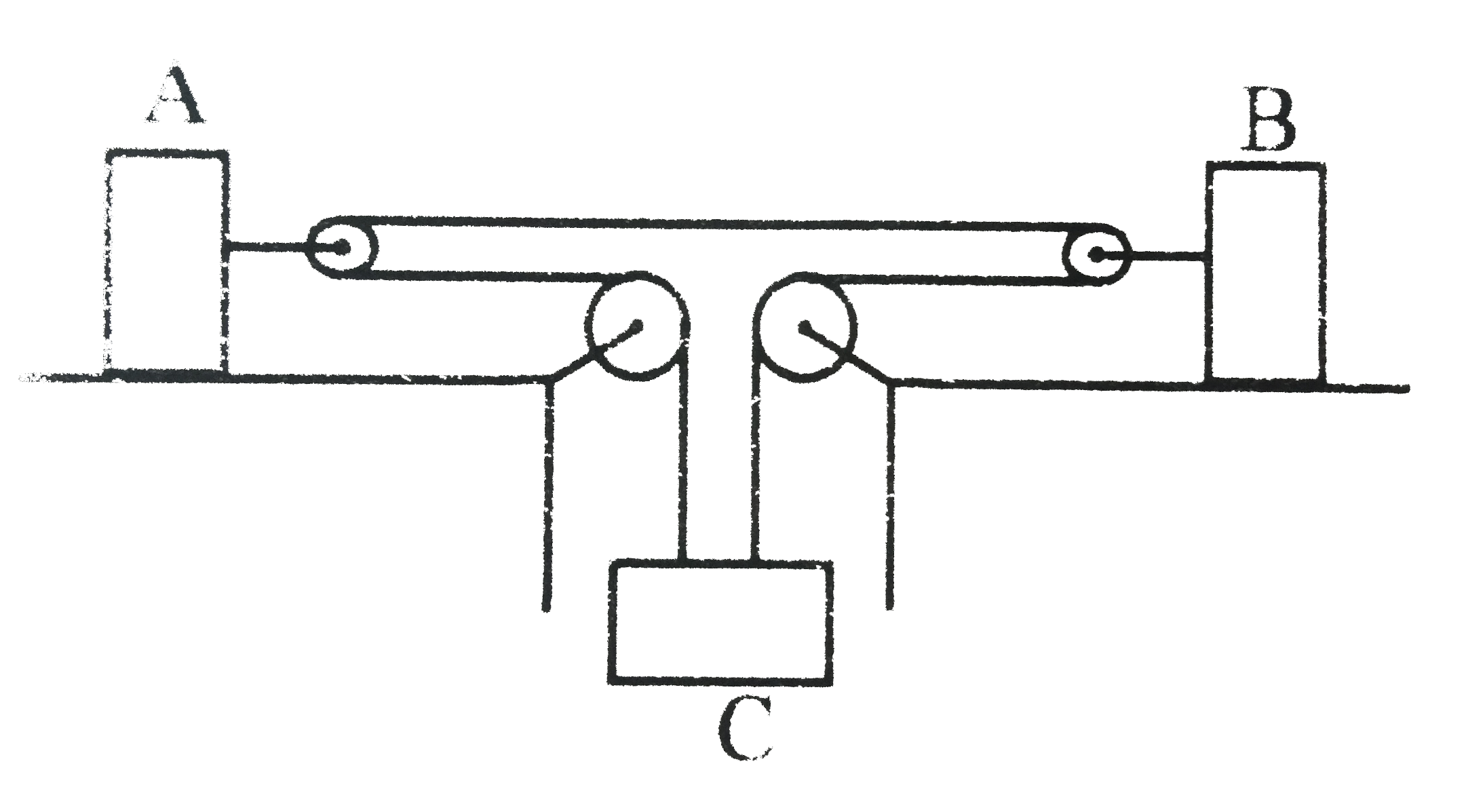
View Solution