A stone is thrown horizontally with a velocity of 10m/sec. Find the radius of curvature of it’s trajectory at the end of 3s after motion began. (g=10m/s2)
10√10m
100√10m
√10m
100m
The correct Answer is:B
Method (I)
After 2sec.
Vy=uy+gt=−30m/s
and Vx=10m/s∴V2=V2x+V2y
⇒V=10√10m/s
Now, tanα=VxVy=13
⇒sinα=1√10
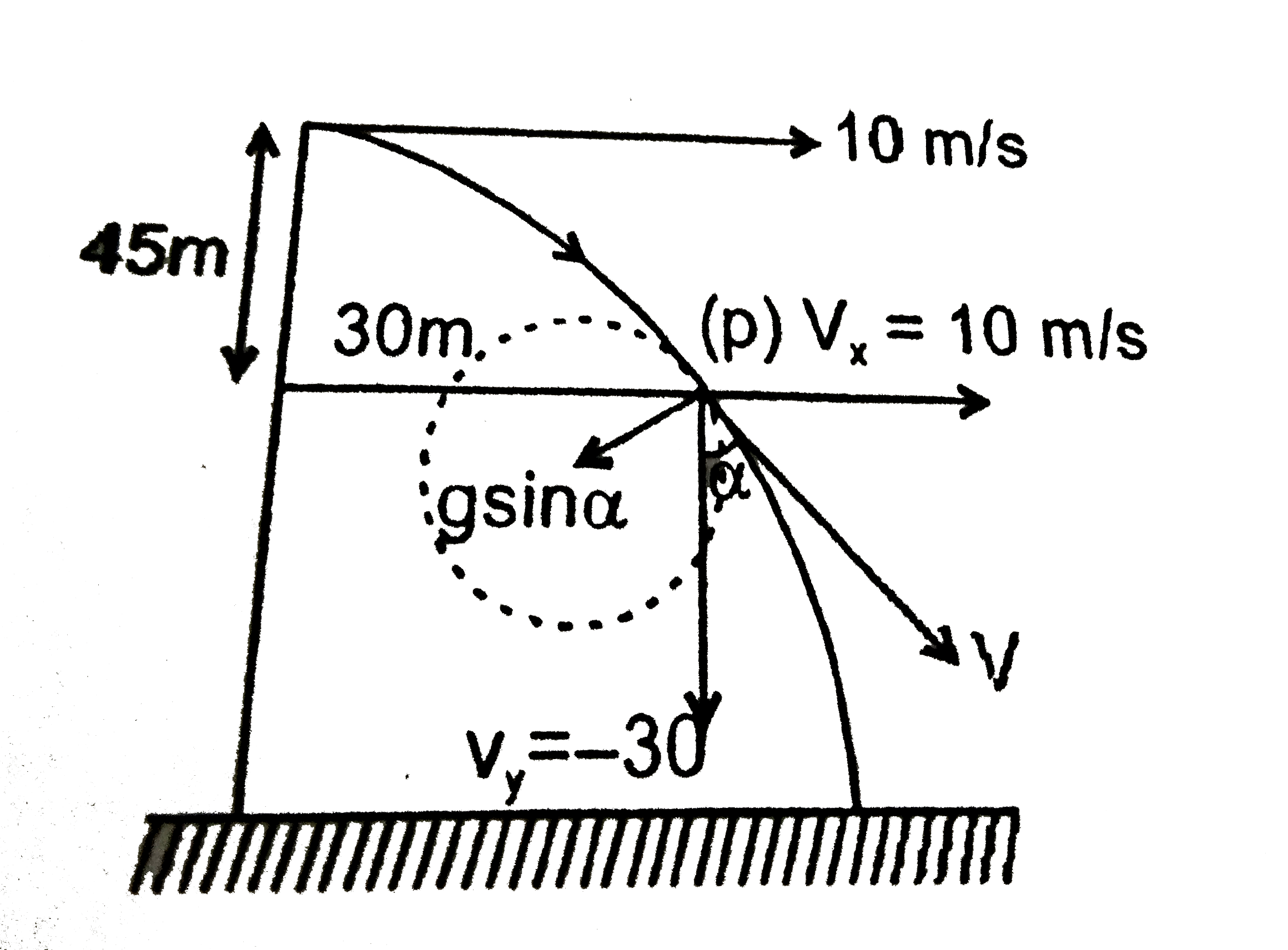
Radius of curvaute r=V2⊥gsinα
r=100√10m
Method (II)
Let horizontal and vertical position of point p be x&y respectively
∴x=Vt and y=12gt2
∴equation of trajectory y=gx22V2
∴dydx=dxV2 and d2ydx2=gV2
Radius of curvature r={1+(dydx)2}3/2d2ydx2
=(1+g2x2V4)3/2g/v2
Now after 3sx=Vt=30m
and V=10m/s
∴r=100√10m.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 42
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 43
11 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 40
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curveture of the trajectory at that point. (Take g=10m/s2)
View SolutionA projectile is fired horizontally with 30m/s from a tower of height 50m .If radius of curvature of trajectory of projectile 3 seconds after projectile is fired,is 180sqrt(k) metres,then value of k is (g=10m/s^(2)
View Solution
Knowledge Check
A stone is thrown horizontally with a velocity of 10m/s at h=0. The radius of curvature of the stone's trajectory at t=3s is : [Take g=10m/s2]
A10√10mB100mC100√10mD1000mA stone of mass 500g is dropped from the top of a tower of 100m height. Simultaneously another stone of mass 1 kg is thrown horizontally with a speed of 10ms−1 from same point. The height of the centre of mass of the above two stone system after 3 sec is (g=10ms−2)
A45 mB35 mC55 mDnone of theseFrom the top of a tower, a particle is thrown vertically downwards with a velocity of 10m/s. The ratio of the distances, covered by it in the 3rd and 2nd seconds of the motion is (Takeg=10m/s2).
A5:7B7:5C3:6D6:3
A body of mass 2 kg is thrown vertically upwards with an initial velocity of 20 m/s. What will be its potential energy at the end of 2 s ? (Assume g=10m/s2).
View SolutionA particle is thrown horizontally from the top of a tall tower with a speed of 10m/s. if radius of curvature of path followed is 4√2k m at t=1sec, then find the value of k.
View SolutionA particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s . After 3s , the magnitude of its displacement is (take g = 10 m/s2)
View SolutionA ballon moves up with a velocity 5m/s. A stone is thrown from it with a horizontal velocity 2m/s relative to it. The stone hits the ground at a point 10m horizontally away from it. (Take g=10m/s2)
View Solution
