Mass Center of a sector of a uniform circular plate
Find location of mass center of a sector of a thin uniform plate.
To find the location of the mass center (centroid) of a sector of a thin uniform plate, we can follow these steps:
1. Understanding the Geometry:
- Consider a sector of a uniform circular plate with a radius R and an angle 2θ.
- The mass center will be located along the axis of symmetry, which is the y-axis in this case. Thus, ycm=0.
2. Define Mass and Area:
- Let σ be the mass per unit area (mass density) of the plate.
- The area A of the sector can be calculated using the formula for the area of a circle sector:
A=12R2⋅2θ=R2θ
3. Calculate Total Mass:
- The total mass M of the sector can be expressed as:
M=σ⋅A=σ⋅(R2θ)=σR2θ
4. Setting Up the Integral for xcm:
- To find the x-coordinate of the center of mass, we use the formula:
xcm=1M∫xdm
- We can consider a differential ring element at a distance r from the center with thickness dr and angle 2θ.
5. Differential Mass Element:
- The mass of the differential ring dm can be expressed as:
dm=σ⋅(2θ⋅r⋅dr)
- Here, 2θ⋅r is the circumference of the ring.
6. Finding x for the Differential Element:
- The x-coordinate of the differential ring is given by:
x=rsin(θ)
7. Substituting into the Integral:
- Now substitute x and dm into the integral:
xcm=1M∫R0(rsin(θ))⋅(σ⋅(2θ⋅rdr))
- This simplifies to:
xcm=2sin(θ)σθM∫R0r2dr
8. Evaluating the Integral:
- The integral ∫R0r2dr evaluates to:
∫R0r2dr=R33
9. Final Expression for xcm:
- Substitute the integral back into the expression for xcm:
xcm=2sin(θ)σθσR2θ⋅R33
- Simplifying gives:
xcm=2Rsin(θ)3
Conclusion:
The location of the mass center of a sector of a thin uniform plate is given by:
xcm=2Rsin(θ)3
- Consider a sector of a uniform circular plate with a radius R and an angle 2θ.
- The mass center will be located along the axis of symmetry, which is the y-axis in this case. Thus, ycm=0.
- Let σ be the mass per unit area (mass density) of the plate.
- The area A of the sector can be calculated using the formula for the area of a circle sector:
A=12R2⋅2θ=R2θ
- The total mass M of the sector can be expressed as:
M=σ⋅A=σ⋅(R2θ)=σR2θ
- To find the x-coordinate of the center of mass, we use the formula:
xcm=1M∫xdm
- We can consider a differential ring element at a distance r from the center with thickness dr and angle 2θ.
- The mass of the differential ring dm can be expressed as:
dm=σ⋅(2θ⋅r⋅dr)
- Here, 2θ⋅r is the circumference of the ring.
- The x-coordinate of the differential ring is given by:
x=rsin(θ)
- Now substitute x and dm into the integral:
xcm=1M∫R0(rsin(θ))⋅(σ⋅(2θ⋅rdr))
- This simplifies to:
xcm=2sin(θ)σθM∫R0r2dr
- The integral ∫R0r2dr evaluates to:
∫R0r2dr=R33
- Substitute the integral back into the expression for xcm:
xcm=2sin(θ)σθσR2θ⋅R33
- Simplifying gives:
xcm=2Rsin(θ)3
The location of the mass center of a sector of a thin uniform plate is given by:
xcm=2Rsin(θ)3
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
In the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
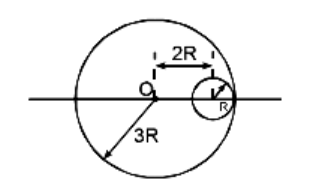 A(a) R2B(b) R5C(c) R4D(d) None of these
A(a) R2B(b) R5C(c) R4D(d) None of these
Locate c.m. of thin , uniform semicircular plate.
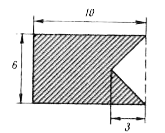
View SolutionFind the center of mass of a uniform plate shown in Fig. 7.10a.
View SolutionFind coordinates of mass center of a quarter sector of a uniform disk of radius r placed in the first quadrant ofa Cartesian coordinate system with centre at origin.
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionLocate the center of mass.

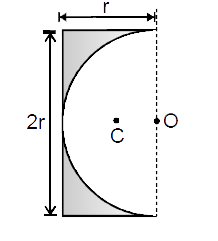
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
View SolutionFrom a uniform circular plate of radius R, a small circular plate of radius R/4 is cut off as shown. If O is the center of the complete plate, then the x coordinate of the new center of mass of the remaining plate will be: X o Y
View Solution
