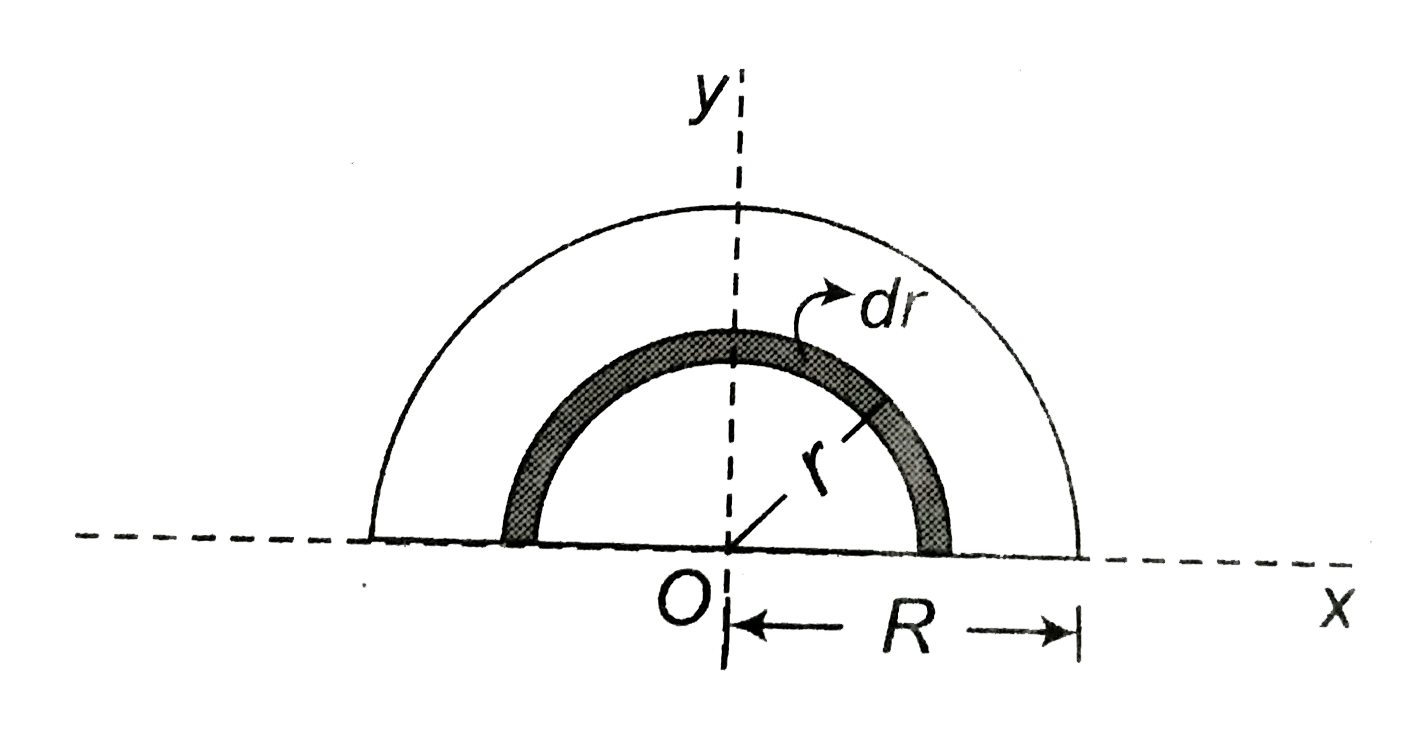
Locate $c . m .$ of thin , uniform semicircular plate.

Video Solution

Text Solution

Verified by Experts

$M a s s / a r e a = \frac{M}{π R^{2} / 2} = \frac{2 M}{π R^{2}}$
Here , the elements is semicircular ring of radius and thickness for
$d A = π r d r$
$d m = \frac{2 M}{π R^{2}} \times π r d r = \frac{2 M}{R^{2}} r d r$
The coordinates of the $c . m .$ of element , $y = \frac{2 r}{π}$
$y_{c . m .} = \frac{\int y d m}{\int d m} = \frac{\int_{0}^{R} \frac{2 r}{π} \frac{2 M r d r}{R^{2}}}{M}$
$= \frac{4}{π R^{2}} \int_{0}^{R} r^{2} d r = \frac{4}{π R^{2}} \frac{r^{3}}{{(3}_{0}^{R}}$
$= \frac{4}{π R^{2}} (\frac{R^{3}}{3}) = \frac{4 R}{3 π}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A folded plate $O A B C D E F O$ made of materials such that part $O A B O$ (say part(i), $B C D O B$ hs mass $4 m, m$ and $m$ respectively. Part (i) is a uniform semicircular plate of radius $R / 2$ and in on the $x y$ plane. Part (ii) and (iii) each is a uniform quarter circular plate of radius $R$ on $x y$ and $x z$ plane respectively. The whole system is free to rotate about $y$ -axis A particle $P$ of mass $m$ moving with velocity $v_{0}$ hits to a point located at the circumcentre of the part (iii) and sticks to it. The point is at a distance $R / 2$ from $x$ -axis as shown in the figure. Angular velocity of the combined system just after the collision is

A $\frac{v_{0}}{4 R}$
B $\frac{2 v_{0}}{5 R}$
C $\frac{3 v_{0}}{5 R}$
D $\frac{v_{0}}{2 R}$
Question 2 - Select One
The moment of inertia of a uniform semicircular disc of mass $M$ and radius $r$ about a line perpendicular to the plane of the disc through the center is
A $\frac{1}{2} M r^{2}$
B $M t^{2}$
C $\frac{2}{5} M r^{2}$
D $\frac{1}{4} M r^{2}$
Question 3 - Select One
The moment of inertia of a uniform semicircular disc of mass disc through the centre is
A $\frac{2}{5} M r^{2}$
B $\frac{1}{4} M r^{2}$
C $\frac{1}{2} M r^{2}$
D $M r^{2}$

CP SINGH-CENTER OF MASS-Exercises

Home
Ask Doubt
Profile