A student throws a horizontal stick of length L up into the air. At the moment it leaves her hand the speed of stick's closes end is zero. The stick completes N turns as it is caought by the student at the initial release point. Find the height h to which the centre of mass of the rod rises.
The correct Answer is:πNL4
Vcm=ωl2
t=2Vcmg=ωlg time of flight
T=2πω time period of one revolution
t=NT ωlg=N2πω
ω2l2=2Nπlg
H=V2cm2g=ω2l24×2g=2Nπlg4×2g=Nπl4
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 68
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 69
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 66
Explore 4 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View Solution
Knowledge Check
A uniform horizontal rod of length l falls vertically from height h on two identical blocks placed symmertrically below the rod as shown in figure the coefficients of restitution are e1 and e2 the maximum height through which the centre of mass of the rod will rise after after bouncing off the blocks is
 Ah(e1+e2)B(e1+e2)2h4C(e1+e2)2h2D4h(e21+e22)
Ah(e1+e2)B(e1+e2)2h4C(e1+e2)2h2D4h(e21+e22)A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)LA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
A2MvM−mB2mvM+mCMvM+mDmvM+m
A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The moment of inertia of the system about the vertical axis passing through the centre of mass C after the collision.
View SolutionA metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.

View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.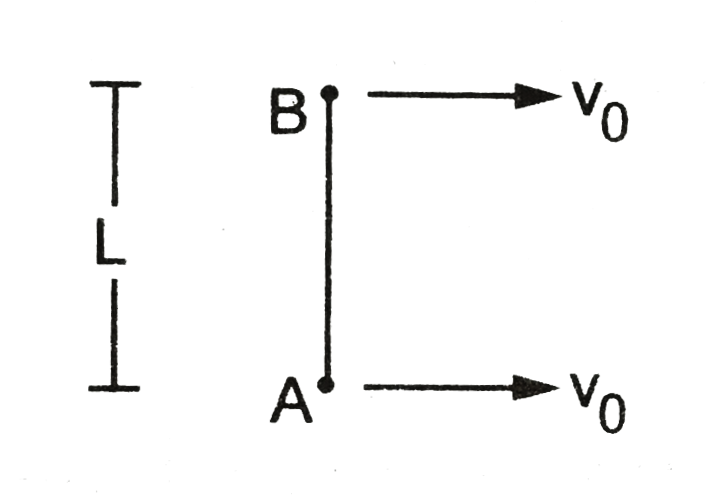
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View Solution

