A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The moment of inertia of the system about the vertical axis passing through the centre of mass C after the collision.
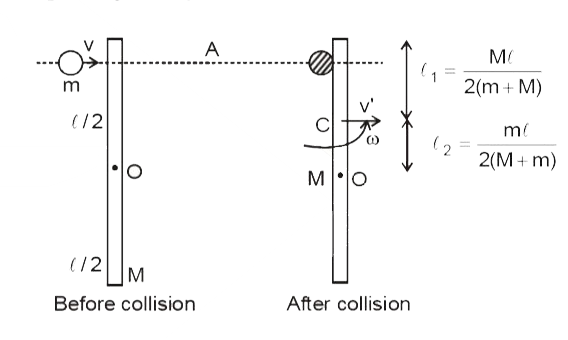
Figure shows the situation of system just before and just after collision.
Initially the centre of mass of the rod is at point O. After collision when the particle sticks to the rod. Centre of mass is shifted from point O to C as shown in figure. Now the system is rotated about axis passing through C
Now from linear momentum conservation
mv=(M+m)v'⇒v'=mvM+m
Let us assume that moment of inertia of the system
about c is . 1 . Then l=l(rod)C+l(part)C
l=l0+Ml22+ml21
l=Ml212+Mm2l24(m+M)2+mM2l24(m+M)2
⇒l=M(M+4m)12(m+M)l2
Topper's Solved these Questions
Similar Questions
A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionSuppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View Solution
Knowledge Check
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)LA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
Aangular velocity of the system after collision is 25vlBangular velocity of the system after collision is v2lCThe loss in kinetic energy of the system as a whole as a result of the collision 310mv2DThe loss in kinetic energy of the system as a whole as a result of the collision 7mv224
A 1m long rod has a mass of 0.12 kg. The moment of inertia about an axis passin through the centre and perpendicular to the length of rod will be
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform bar of length 6a and mass 8 m lies on a smooth horizontal table. Two point-masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively strike the bar as shown in Fig, and stick to the bar after collision.

View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution
