A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
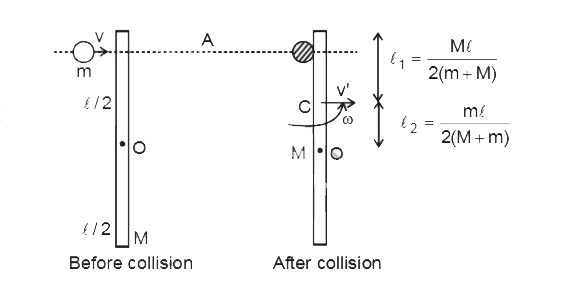
Figure shows the situation of system just before and just after collision.
Initially the centre of mass of the rod is at point O. After collision when the particle sticks to the rod. Centre of mass is shifted from point O to C as shown in figure. Now the system is rotated about axis passing through C
Now from linear momentum conservation
mv=(M+m)v'⇒v'=mvM+m
From Angular momentum conservation about A
Li=Lf
0+0=Iω−(m+M)v'l1
⇒Iω=(m+M)v'l1
Put the value of v',&l1 we get
ω=6mv(M+4m)l
Topper's Solved these Questions
Similar Questions
A uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The moment of inertia of the system about the vertical axis passing through the centre of mass C after the collision.View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L - Question 2 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
A2MvM−mB2mvM+mCMvM+mDmvM+m - Question 3 - Select One
A Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
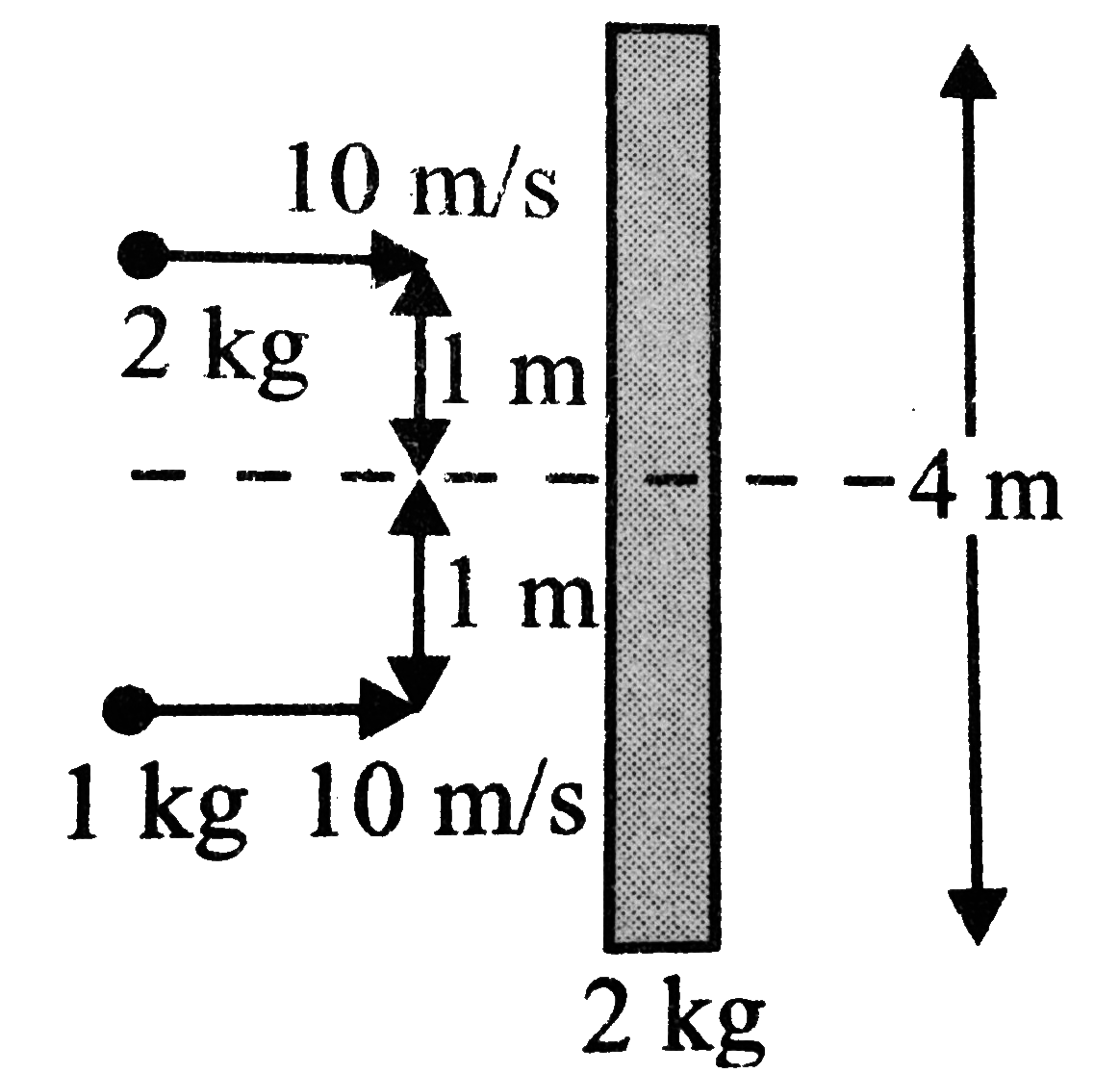
Velocity of the centre of mass of the rod after collision isA12m/sB9m/sC6m/sD3m/s
A uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.View SolutionSuppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively, strike the bar (as shown in figure) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c) total kinetic energy, just after collision.
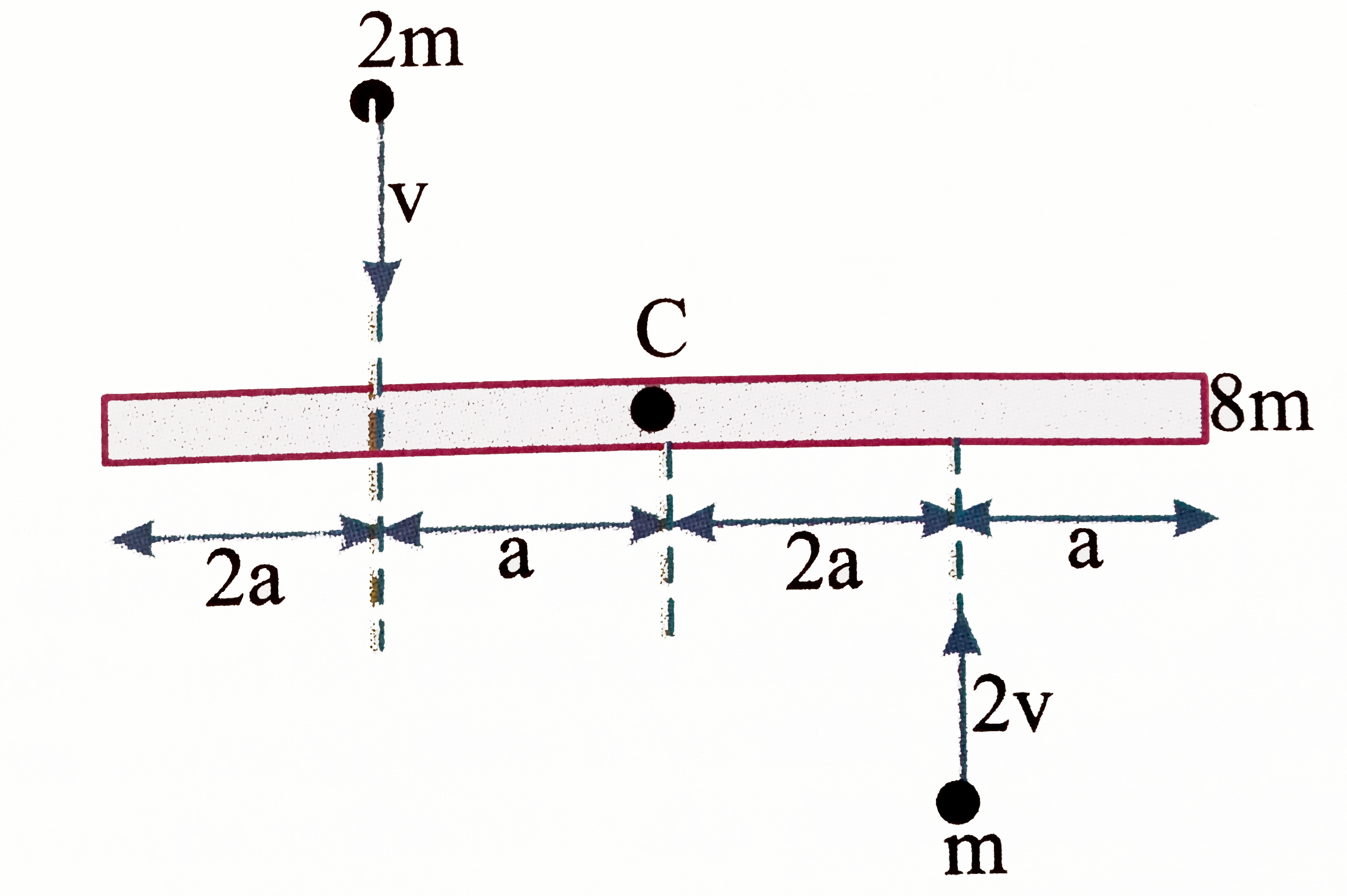 View Solution
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View Solution

