A non uniform cylinder of mass m, length l and radius r having its C.O.M at a distance l4 from centre and lying on axis of cylinder . The cylinder is kept in a liquid of unifrom density ρ. The moment of inertia of the rod about C.O.M is I. The angular acceleration of point A relative to point B just after the rod is released from position shown in figure is .

πρgl2r22I
3πρgl2r24I
πρgl2r2I
πρgl2r24I
The correct Answer is:D
FBuoyancy=πR2lρg
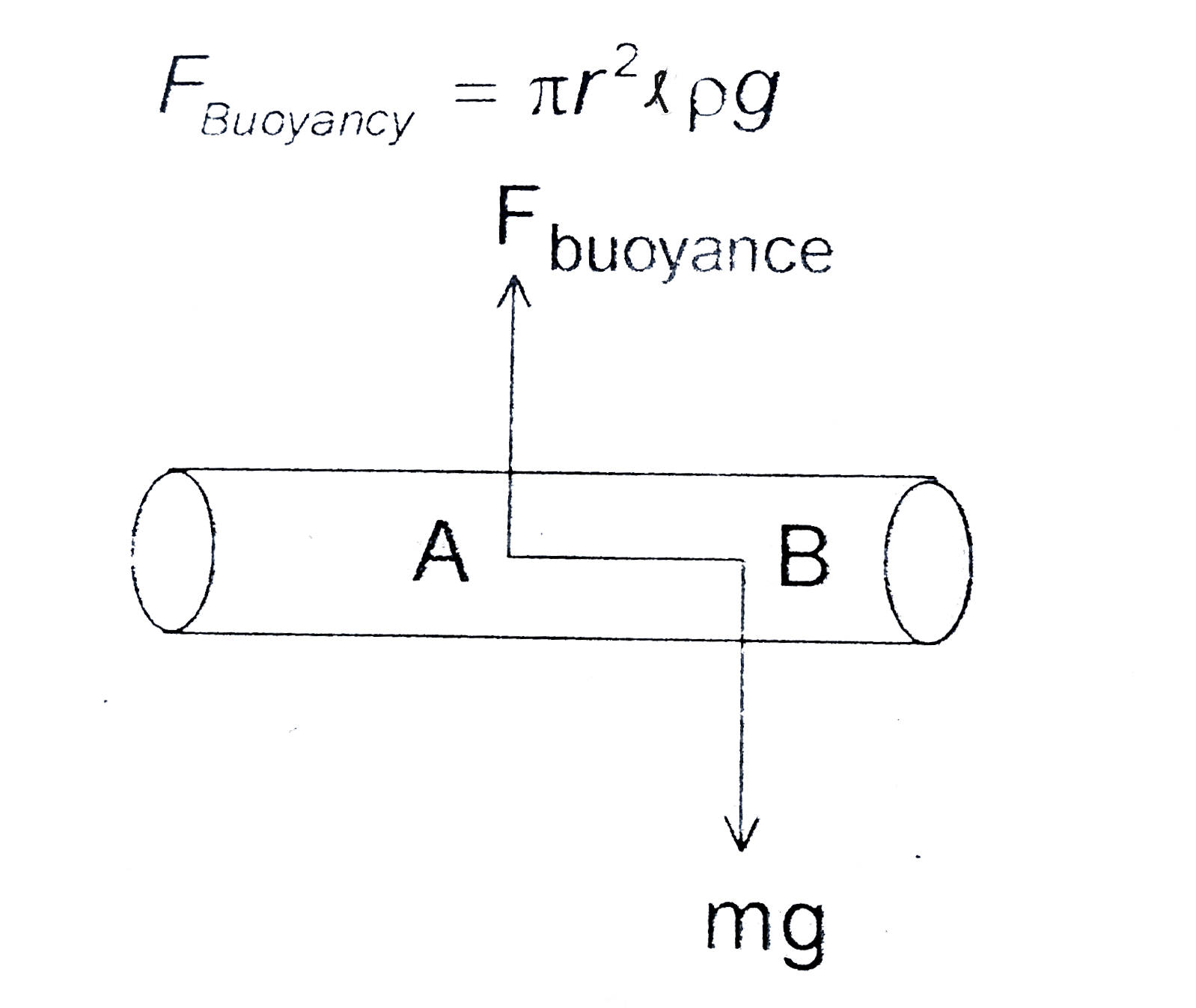
T orque =πr2l2ρg4
α=π2l2ρgr24I
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
Knowledge Check
A non-uniform cylinder of mass m, length l and radius r is having its centre of mass at a distance l.4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is l. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is
 Aπρgl2r2IBπρgl2r24ICπρgl2r22ID3πρgl2r24I
Aπρgl2r2IBπρgl2r24ICπρgl2r22ID3πρgl2r24IMoment of inertia of a hollow cylinder of mass M and radius r about its own axis is
A23Mr2BMr2C13Mr2D12Mr2A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of these
The mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
View SolutionA cylinder of height L, mass M, radius L√2 has MOI 1.2kgm2 about an axis at a distance of L/2 parallel to axis of cylinder. If length of cylinder is 80cm. Find the density of cylinder.
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml2/3, the initial angular acceleration of the rod will be
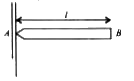
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View Solution
